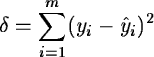
An alternative method performs the interpolation of interorder background using smoothing spline polynomials. Spline interpolation consists of the approximation of a function by means of series of polynomials over adjacent intervals with continuous derivatives at the end-point of the intervals. Smoothing spline interpolation enables to control the variance of the residuals over the data set, as follows:
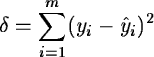
One must retain two particular values of S:
The solution is estimated by an iterative process. Smoothing spline interpolation is designed to smooth data sets which are mildly contaminated with isolated errors. Convergence is not always secured for this class of algorithms, which on the other hand enables to control the residuals. The median of pixel values in a window surrounding the background reference position is computed before spline interpolation. The size of the window (session keyword BKGRAD) is defined along the orders and along the columns of the raw spectrum.