After having crossed an absorbing cloud, the intensity of a source,
I
![]() ,
is received by the observer as I(
,
is received by the observer as I(![]() )
= I
)
= I
![]() ,
where
,
where
![]() is the optical depth of the cloud.
is the optical depth of the cloud.
Let's connect ![]() to the physical parameters.
to the physical parameters.
N : column density
a(: line absorption coefficient
: broadening function
ao =
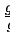
l : lower level of the atomic transition
k : upper level of the atomic transition
: rest wavelength of the transition
gl : statistical weight of the lower level
gk : statistical weight of the upper level
akl : spontaneous transition probability
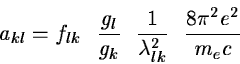
flk = upward oscillator strength