



Next: Correspondence Analysis
Up: Multivariate Analysis Methods
Previous: Cluster Analysis
Discriminant Analysis may be used for two objectives: either
we want to assess the adequacy of classification, given
the group memberships of the objects under study; or we wish
to assign objects to one of a number of (known)
groups of objects. Discriminant Analysis may thus have a
descriptive or a predictive objective.
In both cases, some group assignments must be known before carrying
out the Discriminant Analysis. Such group assignments, or labelling,
may be arrived at in any way. Hence Discriminant Analysis can be
employed as a useful complement to Cluster Analysis (in order to judge
the results of the latter) or Principal Components Analysis.
Alternatively, in star-galaxy separation, for instance, using
digitised images, the analyst may define group (stars, galaxies)
membership visually for a conveniently small training set or
design set.
Methods implemented in this area are Multiple Discriminant Analysis,
Fisher's Linear Discriminant Analysis, and K-Nearest Neighbours
Discriminant Analysis.
- Multiple Discriminant Analysis
- (MDA) is also termed Discriminant
Factor Analysis and Canonical Discriminant Analysis. It adopts a
similar perspective to PCA: the rows of the data matrix to be examined
constitute points in a multidimensional space, as also do the group
mean vectors. Discriminating axes are determined in this space, in
such a way that optimal separation of the predefined groups is
attained. As with PCA, the problem becomes mathematically the
eigenreduction of a real, symmetric matrix. The eigenvalues represent
the discriminating power of the associated eigenvectors. The nYgroups lie in a space of dimension at most nY - 1. This will be
the number of discriminant axes or factors obtainable in the most
common practical case when
n > m > nY (where n is the number of
rows, and m the number of columns of the input data matrix).
- Linear Discriminant Analysis
- is the 2-group case of MDA.
It optimally separates two groups, using the
Mahalanobis metric or generalized distance.
It also gives the same linear separating decision surface as
Bayesian maximum likelihood discrimination in the case of equal
class covariance matrices.
- K-NNs Discriminant Analysis
- :
Non-parametric (distribution-free) methods dispense with the need for
assumptions regarding the probability density function. They have become
very popular especially in the image processing area.
The K-NNs method assigns an object of unknown affiliation to the group
to which the majority of its K nearest neighbours belongs.
There is no best discrimination method. A few remarks concerning the
advantages and disadvantages of the methods studied are as follows.
- Analytical simplicity or
computational reasons may lead to initial consideration of
linear discriminant analysis or the NN-rule.
- Linear discrimination is the most widely used in practice. Often
the 2-group method is used repeatedly for the analysis of pairs
of multigroup data (yielding
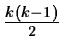 decision
surfaces for k groups).
decision
surfaces for k groups).
- To estimate the parameters required in quadratic discrimination
more computation and data is required than in the case of linear
discrimination. If there is not a great difference in the group
covariance matrices, then the latter will perform as well as
quadratic discrimination.
- The k-NN rule is simply defined and implemented, especially
if there is insufficient data to adequately define sample
means and covariance matrices.
- MDA is most appropriately used for feature selection. As in
the case of PCA, we may want to focus on the variables used in
order to investigate the differences between groups; to create
synthetic variables which improve the grouping ability of the data;
to arrive at a similar objective by discarding irrelevant variables;
or to determine the most parsimonious variables for graphical
representational purposes.




Next: Correspondence Analysis
Up: Multivariate Analysis Methods
Previous: Cluster Analysis
Petra Nass
1999-06-15
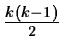 decision
surfaces for k groups).
decision
surfaces for k groups).
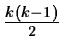 decision
surfaces for k groups).
decision
surfaces for k groups).