 ,
respectively, have particularly simple meanings. It
is transparent that the stochastic signals are analysed more
comfortably in the time domain and periodic signals in the frequency
domain.
,
respectively, have particularly simple meanings. It
is transparent that the stochastic signals are analysed more
comfortably in the time domain and periodic signals in the frequency
domain.
Signals can be classified broadly into deterministic and stochastic signals. A deterministic signal, e.g. a periodic signal, can be predicted for arbitrary spaces of time. For a stochastic signal, no such prediction can be made beyond a certain time interval, called the correlation length lcorr. For any finite time series the classification into these two categories is ambiguous so that methods suitable for both stochastic and periodic signals could be applied to any time series with some success (e.g. quasiperiodic oscillations, Sect. 12.2.6).
Usually processes in the source of the signal (e.g. the nucleus of an
active galaxy) and/or observational errors introduce a random
component into the series, called noise. The analysis of such series
usually aims at removing the noise and fitting a model to the
remaining component of the series. Suitable models can be obtained by
shifting a known series by some time lag, l, or by repeating
fragments of it with some frequency, ![]() .
Accordingly, we are
speaking of an analysis in the time and frequency domain.
In these domains the correlation length lcorr and oscillation
frequency
.
Accordingly, we are
speaking of an analysis in the time and frequency domain.
In these domains the correlation length lcorr and oscillation
frequency  ,
respectively, have particularly simple meanings. It
is transparent that the stochastic signals are analysed more
comfortably in the time domain and periodic signals in the frequency
domain.
,
respectively, have particularly simple meanings. It
is transparent that the stochastic signals are analysed more
comfortably in the time domain and periodic signals in the frequency
domain.
Models usually depend on several parameters. Fitting of the model to
the signal means choosing the best set of these parameters.
Customarily, the observed series, X(o), is split into the modeled series X(m) and the residuals of the observations
with respect to the model,
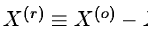 .
.