Next: Multivariate Statistical Methods
Up: Analysis of Results
Previous: Regression Analysis
Often, the computed estimators have to be compared with other values
or model predictions. Different statistical tests are used to compute
the probability of a given hypotheses being correct. A typical null
hypotheses is that two quantities or samples are taken from the same
population. For single quantities, a confidence interval is estimated
for the desired significance level. The null hypotheses is then
accepted at this level of significance if the value is within the
interval. When the underlying distribution is normal, the
``Student's'' t and the 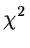 distributions are used to estimate
the confidence intervals for the mean and standard deviation,
respectively.
distributions are used to estimate
the confidence intervals for the mean and standard deviation,
respectively.
It is also possible to test if a set of observed values are taken from
a given distribution.
For this purpose the test variable
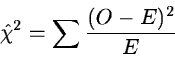 |
(2.34) |
is used where O and E are the observed and expected frequencies,
respectively. The level of significance is derived from
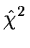 which is
which is 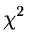 distributed. The bins must be so
large that E is larger than 5 for all intervals.
distributed. The bins must be so
large that E is larger than 5 for all intervals.
When the underlying distribution is unknown, two independant samples can
be compared using the Kolmogoroff and Smirnoff test.
It uses the test variable
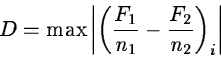 |
(2.35) |
where Fj is the cumulative frequency in the ith interval with
nj values for the two samples j=1,2. The intervals must be of
equal size and have the same limits for both samples. Special tables
give the confidence interval for this test variable. Several other
tests are available for comparing independent samples such as the
U-test of Wilcoxon, Mann and Whitney which uses the rank in its test
variable.




Next: Multivariate Statistical Methods
Up: Analysis of Results
Previous: Regression Analysis
Petra Nass
1999-06-15