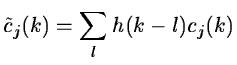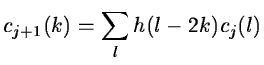Next: Multiresolution with scaling functions
Up: Pyramidal Algorithm
Previous: The Laplacian Pyramid
Pyramidal Algorithm with one Wavelet
To modify the previous algorithm in order to have an isotropic
wavelet transform, we compute the difference signal by:
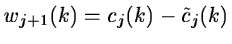 |
|
|
(14.43) |
but
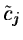 is computed without reducing the number of samples:
is computed without reducing the number of samples:
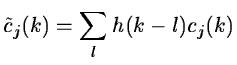 |
|
|
(14.44) |
and cj+1 is obtained by:
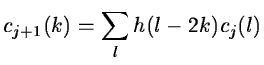 |
|
|
(14.45) |
The reconstruction method is the same as with the laplacian pyramid,
but the reconstruction is not exact. However, the exact reconstruction
can be performed by an iterative algorithm. If P0 represents
the wavelet coefficients pyramid, we look for an image such that the wavelet
transform of this image gives P0. Van Cittert's iterative algorithm gives:
| Pn+1 = P0 + Pn - R(Pn) |
|
|
(14.46) |
where
- P0 is the pyramid to be reconstructed
- Pn is the pyramid after n iterations
- R is an operator which consists in doing a reconstruction followed
by a wavelet transform.
The solution is obtained by reconstructing the pyramid Pn.
We need no more than 7 or 8 iterations to converge. Another way to
have a pyramidal wavelet transform with an isotropic wavelet is
to use a scaling function with a cut-off frequency.




Next: Multiresolution with scaling functions
Up: Pyramidal Algorithm
Previous: The Laplacian Pyramid
Petra Nass
1999-06-15