



Next: The Wiener-like filtering in
Up: Noise reduction from the
Previous: Noise reduction from the
We will examine here the computation of a convolution
by using the continuous wavelet transform in order to get a framework for
linear smoothings. Let us consider the
convolution product of two functions:
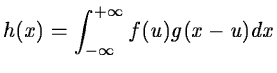 |
|
|
(14.68) |
We introduce two real wavelets functions 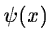 and
and 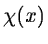 such that:
such that:
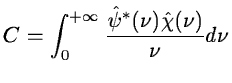 |
|
|
(14.69) |
is defined.
Wg(a,b) denotes the wavelet transform of g with the wavelet
function 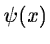 :
:
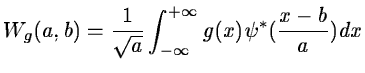 |
|
|
(14.70) |
We restore g(x) with the wavelet function 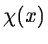 :
:
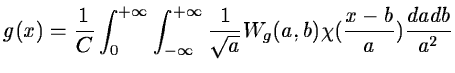 |
|
|
(14.71) |
The convolution product can be written as:
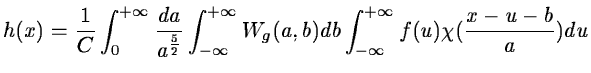 |
|
|
(14.72) |
Let us denote
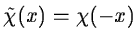 .
The wavelet transform Wf(a,b) of f(x) with
the wavelet
.
The wavelet transform Wf(a,b) of f(x) with
the wavelet
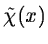 is:
is:
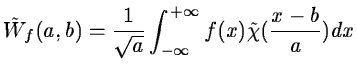 |
|
|
(14.73) |
That leads to:
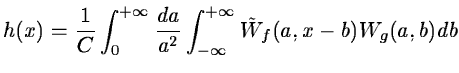 |
|
|
(14.74) |
Then we get the final result:
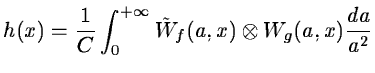 |
|
|
(14.75) |
In order to compute a convolution with the continuous wavelet
transform:
- We compute the wavelet transform
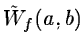 of the function f(x) with the
wavelet function
of the function f(x) with the
wavelet function
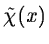 ;
;
- We compute the wavelet transform Wg(a,b) of the function g(x) with the
wavelet function
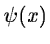 ;
;
- We sum the convolution product of the wavelet transforms, scale by scale.
The wavelet transform permits us to perform any linear filtering.
Its efficiency depends on the number of terms in the wavelet
transform associated with g(x) for a given signal f(x). If we
have a filter where the number of significant coefficients is
small for each scale, the complexity of the algorithm is
proportional to N. For a classical convolution, the complexity
is also proportional to N, but the number of operations is also
proportional to the length of the convolution mask. The main
advantage of the present technique lies in the possibility of having a
filter with long scale terms without computing the convolution on
a large window. If we achieve the convolution with the FFT
algorithm, the complexity is of order 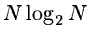 .
The computing time is
longer than the one obtained with the wavelet transform if we
concentrate the energy on very few coefficients.
.
The computing time is
longer than the one obtained with the wavelet transform if we
concentrate the energy on very few coefficients.




Next: The Wiener-like filtering in
Up: Noise reduction from the
Previous: Noise reduction from the
Petra Nass
1999-06-15
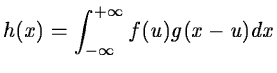
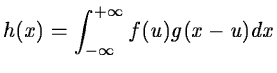
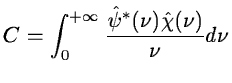
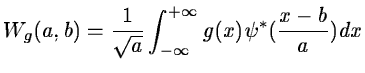
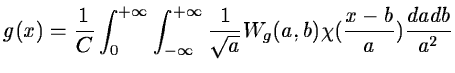
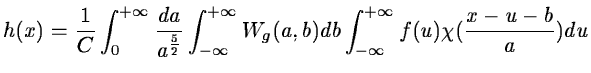
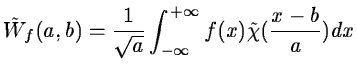
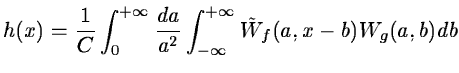
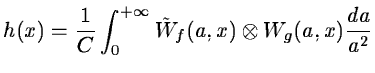
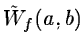 of the function f(x) with the
wavelet function
of the function f(x) with the
wavelet function
![]() .
The computing time is
longer than the one obtained with the wavelet transform if we
concentrate the energy on very few coefficients.
.
The computing time is
longer than the one obtained with the wavelet transform if we
concentrate the energy on very few coefficients.