 is continuous in parameter space. Problems may arise if local minima
occur for ``reasonable'' values of parameters and methods need to be
employed to search for absolute minima.
is continuous in parameter space. Problems may arise if local minima
occur for ``reasonable'' values of parameters and methods need to be
employed to search for absolute minima.
 )
to measure the discrepancy between
observations and hypothesis can be found in many excellent text books
(see e. g. Bevington, 1969). Hence, it is not really useful to give
any theoretical summary here.
)
to measure the discrepancy between
observations and hypothesis can be found in many excellent text books
(see e. g. Bevington, 1969). Hence, it is not really useful to give
any theoretical summary here.
Although minimisation of the absolute deviations or, more precisely,
the square of deviations between data and a parametric model is not
the only technique to derive optimum values for parameters, it is
generally used because it is straightforward and theoretically justified.
There are no basic difficulties in extrapolating this method for the
case of a model function with non-linear parameters if  is continuous in parameter space. Problems may arise if local minima
occur for ``reasonable'' values of parameters and methods need to be
employed to search for absolute minima.
is continuous in parameter space. Problems may arise if local minima
occur for ``reasonable'' values of parameters and methods need to be
employed to search for absolute minima.
Nevertheless, if the PSF parameters are reasonably estimated one can assume that the localisation of the region of absolute minimum is generally well determined. This is an important condition since the method ROMAFOT uses requires that high order terms in the expansion of the fitting function are negligible, a condition satisfied if the starting point is close to the minimum.
This method is to expand the fitting function to first order in a Taylor
expansion, where the derivatives are taken with respect to the parameters
and evaluated for the initial guess in this space. The calculation of the
model parameters to fit the data has led to the solution of the usual
system:
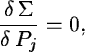
Using the technique just outlined, ROMAFOT carries out stellar photometry by fitting a sum of elementary Point Spread Functions, analytically determined, to a two dimensional array. The sky contribution is taken into account with an analytical plane, possibly tilted. This plane is fitted (simultaneously) with the stars.
The analytical formulation of the PSF has obvious advantages in case of undersampled images allowing the comparison of the intensity of each pixel to the integral of the function over the pixel area. ROMAFOT does not attempt to discriminate between stars and galaxies in the phase of searching the objects. It prefers to take into account their photometric contribution and delete them from the final catalogue by checking the fit parameters with a suitable program. This program also eliminates cosmic rays and defects, if present.
In several parts in this documentation reference is made to the sigma
(![]() )
of either the Gaussian or the Moffat fitting function. In
both cases this sigma is NOT the sigma in the statistical sense
(i.e. the standard deviation) but the Full Width Half Maximum (FWHM)
of the distribution. In case of the Moffet distribution, sigma is a
function of the parameter
)
of either the Gaussian or the Moffat fitting function. In
both cases this sigma is NOT the sigma in the statistical sense
(i.e. the standard deviation) but the Full Width Half Maximum (FWHM)
of the distribution. In case of the Moffet distribution, sigma is a
function of the parameter ![]() ,
i.e. not equal to the FWHM except
for
,
i.e. not equal to the FWHM except
for ![]() .
This definition of sigma will be used throughout this
chapter.
.
This definition of sigma will be used throughout this
chapter.