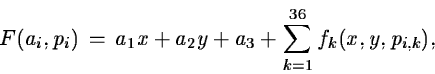
This command determines the characteristics (position, width, height) of each selected stellar object through a non-linear best fit to the data. It assumes that a Gaussian or a Moffat function is adequate to describe the PSF and that a (possibly tilted) plane is a good approximation of the sky background.
This command can be used for many purposes. For instance, the shape of the object can be determined by performing a best fit with all parameters allowed to vary; alternatively, a complex object (e.g. a blend of ten or more objects) can be reconstructed using some a priori knowledge, such as the width of the PSF or the positions. In the first case, an object with an informative content which is as high as possible is necessary to settle the parameters involved; in the latter case this information is added to the data having a low degree of information.
Experience has shown that a Moffat function with appropriate parameters
is always able to follow the actual profile of the data satisfactorily;
a Gaussian is adequate in case of poor seeing. In general the fitting
function can be described by the expression:
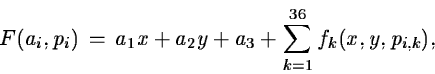
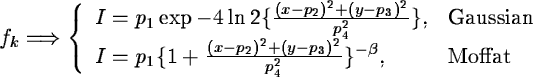
Besides the best fit, FIT/ROMAFOT also computes the quality of
the fit by the  test and the semi-interquartile interval
for each individual object. These data are stored together with the fit
parameters and will be used by other commands (see EXAMINE/ROMAFOT).
test and the semi-interquartile interval
for each individual object. These data are stored together with the fit
parameters and will be used by other commands (see EXAMINE/ROMAFOT).
During the execution the user will realise that the command occasionally makes several trials on the same window. This happens when the command is requested to fit a window with several objects and when one or more of these falls into the category ``NO CONVERGENCY''. In this case the command continues by ignoring such objects. When finally the convergency is found, the objects so far ignored are added and a new trial will start. The program will never delete objects on its own. The only exception is if an object falls under the threshold selected by the user, and after the background has been properly calculated considering, for instance, ``tails'' of nearby stars.
It should be emphasised that, even if the window is marked ``NO CONVERGENCY'', some objects in that window (in general the most luminous ones) have been found with adequate convergency. These objects will be flagged ``1'', while the objects flagged ``3'', ``4'' or ``5'' will be those responsible for ``NO CONVERGENCY''. Finally, objects flagged ``0'' are those under the photometry threshold. These flags should not worry the user; they will be used by subsequent commands. Now, the trial values contained in the intermediate table have been substituted by the result of fit in each record. To check their quality interactively in order to define the PSF, the user should execute the next command.