[Top] [Prev] [Next] [Bottom]
13.3 Resolving Structure with TRANSFER Mode
TRANSFER mode observations with the FGS can resolve the individual components of multiple star systems and measure the angular diameters of extended objects. These observations scan the instantaneous field of view (IFOV) of the FGS across an object to accumulate the necessary data for a post observation reconstruction of the x and y axis S-curves. The GO compares the observed S-curves to those from a reference star in the calibration database to deconvolve the contribution from each component of a multi-star system or each chord of an extended object. Such an analysis can reveal the magnitude difference and relative separation of a binary star system or the apparent angular diameter of an extended object in both the x and y directions.
Routine pipeline processing of TRANSFER mode data, discussed in Chapter 11 is confined to locating the individual scans within the data files, editing out bad data, and computing guide star centroids and standard deviations during each scan. Otherwise TRANSFER mode observations have always been processed interactively rather than through a pipeline, which is why we discuss them here as a form of FGS data analysis. In the near future the pipeline will be upgraded to perform extensive data reductions on TRANSFER mode observations (see Chapter 11) in order to support the mixed-mode approach, which combines TRANSFER mode observations with POSITION mode observations made in the same visit. More specifically, the pipeline modifications will enable the results from TRANSFER mode observations to be used along with the POSITION mode observations in the construction of virtual plates. The ultimate goal is to support the scientific determination of parallaxes, proper motions, and reflex motions due to dark companions of multi-star systems resolvable with the FGS.
13.3.1 FGS Response to a Binary
In their purest form, TRANSFER mode observations are made to resolve a close binary pair, to monitor it over time, and to derive its orbit. Unlike radial velocity studies, an orbit determined by the FGS reveals the system's inclination. Additional information about the system's parallax or radial velocities can be used to determine its masses. In order to clarify how TRANSFER mode observations determine binary separations and relative intensities, we will first discuss the response of the Koester prisms to the wavefront from a binary star.
The wavefront of a point source at the face of a Koester prism is colliminated, coherent, polarized, and characterized by a propagation vector. As the instantaneous field of view of the FGS scans across the target, the tilt of the wavefront varies and the PMTs register different relative intensities. Plotting the position of the IFOV along the scan path against the normalized difference of the PMTs thus reveals the characteristic S-curve of the FGS (see "S-curves" on page 9-8).
If the source is a double star, then its wavefront at the face of the Koester prism will have two components, each coherent with itself but incoherent with respect to the other. Two propagation vectors characterize this wavefront and the angle between them is directly related to the angular separation of the stars on the sky. As the FGS's IFOV scans across the object, each component of the wavefront generates its own S-curve, whose modulation is diminished by the non-interfering background contribution from the other component. The interferometric null for each star occurs at a different point along the scan path, so the resulting relationship between the position of the IFOV along the scan path to the normalized difference of the PMTs depends upon both the separation of the stars and their relative brightnesses. To demonstrate this effect, Figure 13.4 shows the FGS 3 y-axis S-curves of several synthetic binary systems with a variety of angular separations and relative intensities.
Figure 13.4: Effect of Double Stars on S-curve 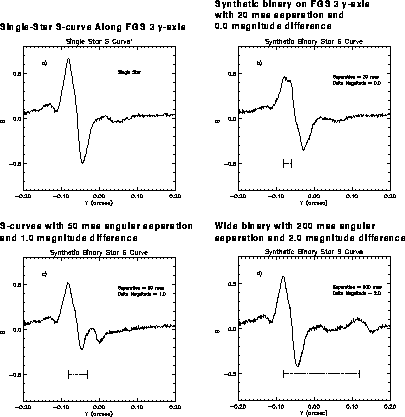
Figure 13.5: Resolving Power of FGS 3 Dependency on Characteristics of Single Star S-curves. Note that the x-axis S-curve in (d) "looks" more like the single star s-curve in (a) than does its cousin along the y-axis, demonstrating the enhanced resolving power along the y-axis relative to that along the x-axis. 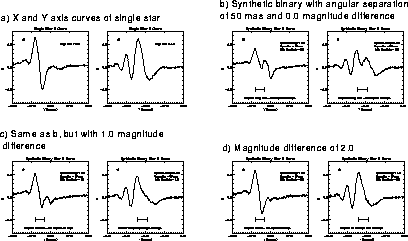
If the angular separation of the stars is greater than the characteristic width of an S-curve, two distinct S-curves will be apparent, but the modulation of each will be diminished relative to that of a single star by an amount depending on the relative intensity of each star. On the other hand, if the angular separation is sufficiently small, the S-curves will be superimposed, and the morphology of the resulting blend will be complicated. In either case, the composite S-curve can be deconvolved using reference S-curves from point sources, provided the angular separations are not too small and the magnitude difference is not too large. To be more precise, fitting the observed double star S-curve with two appropriately weighted, linearly superimposed reference S-curves from single stars can determine the angular separation and magnitude difference of the binary's components.
The modulation and morphology of its point-source S-curves ultimately determines the resolving power of the FGS. Figure 13.5 diagrammatically demonstrates how the amplitude of the S-curve couples with the magnitude difference of the binary to determine the FGS's resolving power. It shows a synthetic binary star system with an angular separation of 50 mas on both the x and y axes of FGS 3, but at a variety of relative intensities. It is clear that as the magnitude difference increases, the resolving power of the FGSs along the x-axis becomes doubtful well before that of the y-axis. Note, however, that this separation and selection of magnitude differences was chosen solely for its visual impact. The data reduction algorithm would have no difficulty resolving the binary in Figure 13.5c.
13.3.2 TRANSFER Mode Data Reduction
After the astrometry pipeline locates and extracts the individual scans of a TRANSFER mode observation, the resulting data files are ready for further analysis. Currently, the steps involved in routine TRANSFER mode data reduction are:
- Visual inspection of the S-curves from each scan to identify and disqualify those corrupted by vehicular jitter or data dropouts.
- Dejittering of the astrometry data at 40 Hz using the instantaneous position of the dominant guide star in its FGS, if desired. (This step may requalify scans that would otherwise be deleted from further consideration.)
- Cross-correlation of each scan, in order to detect any drift of the FGS across the sky during the course of the observation.
- Shifting of each scan by the amount determined necessary in step (3) so that all scans are mapped to a common reference frame.
- Binning and co-adding of the individual scans to generate a high signal to noise composite S-curve. Each step of the IFOV along each scan is placed into an appropriate bin, and then all entries in a given bin are averaged to produce the high S/N binned and co-added S-curve. See Figure 13.6.
- Fitting of a piecewise third order polynomial fit to the binned and co-added S-curve.
Figure 13.6: Benefits of Binning and Co-adding of Individual Scans 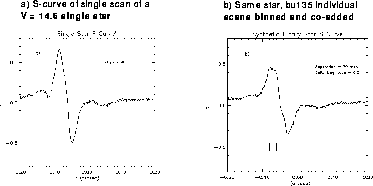
If the observation is a calibration measurement, the goal of the calibration proposal will drive the subsequent analysis of the data by the FGS group at STScI. For example, if the object was observed to obtain a color calibration of a single star, the data will be inspected to assure that the object does in fact appear to be single star. If so, the raw and processed data will be entered into the FGS calibration database and be made available to the observer.
If the observation under analysis is of a binary star system and the observer wishes to determine the angular separation and magnitude difference of its components, the following additional tasks are undertaken.
- Selection of an appropriate set of reference S-curves from the calibration library on the basis of the target color (or colors) and the dates of observation of both the binary system and the calibration stars. These dates should be as close as possible to minimize the impact of temporal variations in FGS3.
- Fitting the binary system's composite S-curves with the reference S-curves by iteratively determining the angular separation and magnitude difference. This fitting is done on both the x and y axis. The quality of the fit can be assessed by comparing the magnitude differences determined independently along each axis.
On the other hand, if the observed target is an extended object, the GO will retrieve the appropriate reference S-curves from the calibration data base and use software tools appropriate for such an investigation.
Whether the observation be of a calibration star, a binary system, or an extended source, STScI will be producing publically available software packages to support the analysis of these data. Please consult the STScI FGS Web pages for updates.
13.3.3 Uncertainties in TRANSFER Mode Data
This section discusses several error sources associated with analysis of TRANSFER mode data:
Spacecraft Jitter
When the FGS is used as an astrometer in TRANSFER mode the observer specifies several individual scans of the target in a particular visit, typically between 15 and 35. Periods of extreme spacecraft jitter or telemetry dropouts can compromise the data from an individual scan. Mild jitter of the spacecraft, at the level of 20 mas peak-to-peak, is repairable by using the guide star data to remove the apparent wobble of the sky in the astrometer's aperture. In the most extreme cases, it may be necessary to disqualify a number of scans from further analysis.
To obtain high signal-to-noise S-curves, the single scans must be cross-correlated, shifted, binned, and co-added. Any small, unaccounted for spacecraft motion that occurs during each scan will effectively blur the boundaries of the binning procedure, ultimately causing the co-added S-curve to suffer some loss of spatial resolution. This effect invariably occurs because even a 40 Hz de-jittering of an astrometry observation executed during the quietest of HST orbits will not escape the residual jitter introduced into the pointing control system by the guide stars' photometric noise. Thus, the maximum resolving power of an FGS in TRANSFER mode can not be better than about 1 mas. Figure 13.7 compares the S-curves from two single scans, one obtained during a nominally quiet HST pointing, and the other observed during a time of high spacecraft jitter.
Figure 13.7: Comparison of S-curves from Two Separate Scans during Same Observation 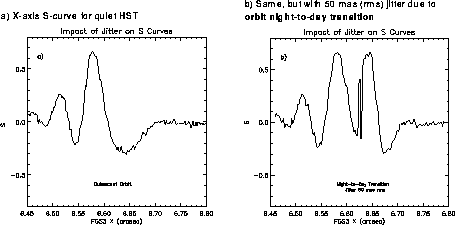
FGS Drift
As discussed in the calibration chapter, astrometry stars observed in POSITION mode more than once in a given visit reveal that the FGS's total field of view drifts across the sky over the course of an HST orbit. This drift is also apparent in TRANSFER mode observations. The cross-correlation of S-curves prior to binning and co-adding automatically accounts for drift in TRANSFER mode observations. Each single-scan S-curve is shifted so that the particular feature of the S-curve used for the cross correlation coincides with that of the fiducial S-curve. The reliability of implicitly removing the drift is only as good as the accuracy of the cross correlation procedure.
Proper cross correlation is relatively straightforward for bright objects (V < 13), but for fainter objects it becomes more difficult, just as binning and co-adding becomes all the more important. In such cases it might be advantageous to construct a drift model iteratively by time tagging the shifts determined by the cross-correlation procedure. Fitting of these shifts to a linear or quadratic drift model might align the individual S-curves more reliably than a procedure that depends solely on individual noisy scans. For bright stars with V < 13, drift in the FGS is estimated to degrade the resolution of TRANSFER mode observations by about 1 mas. For fainter stars, the degradation will increase significantly in a way that depends on details of HST's orbital environment during the visit. Recall from the discussion of drift on page 12-12 that its origin is not well understood. It is not repeatable, and its amplitude depends weakly upon the declination of HST's V1 axis. If a particular observation of a faint star (V > 15) was subject to typical drift of around 10 to 12 mas, then the estimated loss of angular resolution would be about 4 mas.
Temporal Variability of S-Curves
Measurements of the standard star Upgren69 over the lifetime of FGS3 have indicated 1-2% temporal variability of the shapes and the peak-to-peak amplitude of its S-curves. The magnitudes of these changes can have important consequences in the reduction of binary star data when the separation of the components is less than 20 mas and the magnitude difference exceeds 0.6. These temporal changes also affect analyses of extended source observations. There are three ways to minimize the effects of temporal S-curve instability:
Figure 13.8: Temporal Changes in FGS3's x and y axis S-curves from 6/94 to 9/95 to 10/96). Notice the larger changes along the x-axis while the y-axis remains quite stable.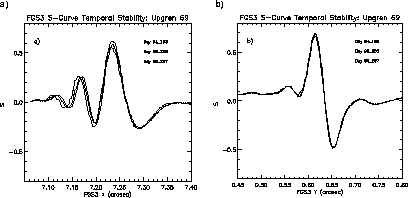
Wavelength Dependence of S-Curves
S-curves are also wavelength dependent. Semi-empirical modeling has shown that when the difference between a standard reference star color and the target star color, delta (B-V), exceeds 0.2-0.3 magnitudes, the residuals of the deconvolution begin to degrade the reliability of the binary star analysis. To deconvolve a binary system, reference scans of the appropriate colors, scaled by the relative brightnesses, are required. Models and extrapolations have yet to reproduce this wavelength dependence of the FGS S-curves with acceptable accuracies. The optical train is very complex, and the database of reference transfer functions to date is not comprehensive. The current STScI calibration program includes observations of single reference stars whose colors are comparable, within 0.2-0.3 magnitudes, to the targets in the GO programs. These are observed about once per cycle and are available in the standard reference library. As we build up this color library, we will investigate further these effects, and the possibilities for improved modeling, with the objective of providing observers the means to generate a single-star reference S-curve for exactly the color required. Figure 13.9 shows how the S-curves in FGS3 respond to the color of the object. Note that both the x and y S-curves respond to the color effect, unlike the temporal changes which affect mostly the x-axis.
Figure 13.9: Effects of Star Color on FGS S-curves 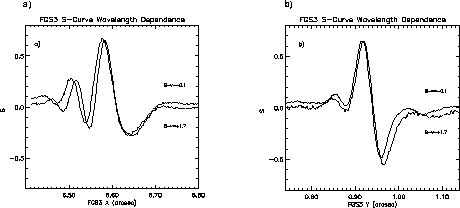
TRANSFER Mode Plate Scale and HST Roll
Several observing programs have revealed that the measured separation of a binary system is sensitive to its orientation relative to the FGS interferometer axis. The impact of this dependence on the HST roll angle is to introduce systematic variations into the binary's orbit. In some cases, these variations could masquerade as perturbations by massive dark companions. Hughes Danbury Optical Systems has developed a model for this effect, which involves a linear relation between the separation of the components derived from the S-curves and the roll at which the data were obtained. The error is a few percent (< 3%) of the separation, scaling linearly with separation, so binaries with large separations (> 200 mas) are affected more than those with small angular separations.
This effect is believed to be due to a rotation of the Koester prism about the normal to its entrance face. The Cycle 7 calibration program incorporates a test that will be used to verify and fine-tune this model, and the results will be made generally available as an STSDAS calibration tool. Check the STScI FGS WWW pages for updates.
[Top] [Prev] [Next] [Bottom]
stevens@stsci.edu
Copyright © 1997, Association of Universities for Research in Astronomy. All rights
reserved.
Last updated: 11/12/97 07:58:42





