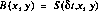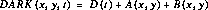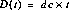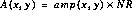[Top] [Prev] [Next] [Bottom]
17.2 Dark Current Subtraction Errors
17.2.1 Dark Current Pedestal
NICMOS data show what is known as the dark current pedestal. This is an additive signal that appears whenever the detector's amplifiers are switched on, which happens at the beginning of an observing sequence, after a filter wheel motion, spacecraft motion, or Earth occultation. The level of the pedestal is quadrant-dependent and random, with typical values below 40-50 DN.
At the time of writing (August 1997) a flight software modification is being developed to remove the pedestal. The basic idea is to leave the amplifiers on at all times (instead of keeping them off, and switching them on only when exposures start). The degree to which this strategy has succeeded will not be known for some time after the change is made.
Being an additive signal, the most noticeable effect of the pedestal is to leave flatfield residuals in the calibrated images; the pedestal is a uniform offset without any flatfield variations, and so the flatfield correction step in calnica will impose an inverted flatfield response pattern in the final calibrated image. In addition, the absolute photometry of extended objects (i.e., those for which a reference sky level cannot be obtained within the frame) will be altered. Finally, the presence of the pedestal makes the calnica automatic cosmic ray rejection processing of MULTIACCUM images less effective. Since currently the pedestal effect lacks full characterization, it cannot be calibrated out by the pipeline.
For observations of compact sources, where most of the frame is occupied by blank sky, an iterative procedure can be used to remove most or all of the pedestal. The procedure exploits the large scale non-uniformity of the NICMOS flatfields, which will produce a large scale modulation of the blank sky in a calibrated NICMOS image with a considerable pedestal signal. The goal of the procedure is to remove the pedestal by minimizing the flatfield non-uniformities. This technique was thought out and developed by Mark Dickinson of the Johns Hopkins University, and is outlined below.
The procedure is iterative and identifies the minimum of the residual flatfield non-uniformities on the calibrated images (run through calnica, only). It should be applied on a quadrant-by-quadrant basis, becuase the pedestal level is different in different quadrants. For MULTIACCUM data, the procedure should be applied on individual imsets; however, it is not useful for the very first few readouts (where there is very little signal), and as a rule of thumb should be applied to those imsets with exposure times greater than about ten seconds. Increasing values of the pedestal level are subtracted from the each quadrant in the raw images, and the latter are run through the calibration software calnica, up to the flatfielding step only. The calibrated images are then smoothed (e.g., using the IRAF tool rmedian) to remove sources and pixel-to-pixel variations of the flatfield residuals. Finally, the variance of the residual large-scale modulation in each image is computed relative to the appropriate constant sky level. The pedestal level which yields the minimum for the variance is selected as the value for that particular quadrant. Because the reference value for the image is a constant sky level, it is clear why this technique can be applied only to those frames containing a large fraction of blank sky.
17.2.2 Synthetic MULTIACCUM Darks
NICMOS dark images are highly dependent on the readout history of the array since it was last reset, and, therefore, cannot be simply rescaled to the exposure time of the science data (as is done with most conventional CCD data). Each science file must be calibrated with a dark frame of equal exposure time and number of readouts.
A NICMOS dark frame can be decomposed into three basic components:
Dark Current
The dark current component is the detector current when no external signal is present. This component is a function of time only: 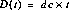
Where D is the observed signal in a given readout, t is time since reset, and dc is the dark current (e-/s). The NICMOS dark current is of the order of 0.05-0.06 e-/sec for Camera 2, and < 0.03 e-/sec for Cameras 1 and 3.
Amplifier Glow
The characteristics of the amplifier glow are described in the section "Instrument Artifacts" on page 17-11. For the purpose of dark frame modelling, it is enough to know that the amplifier glow is a signal: infrared radiation emitted by the amplifiers at the four corners of each NICMOS array, which is detected by the pixels in the array. It is like having a small light bulb in each corner, which produces a pattern of light that is highest in the corners and decreases towards the center of the array. Because the signal is injected in the array every time this is read, the amplifier glow depends on the number of readouts performed in a particular exposure. In particular, it is proportional to the number of readouts since the last reset: 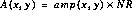
where A(x,y) is the cumulative signal due to the glow in a sequence, amp(x,y) is the amplifier glow signal per readout (a function of the pixel location x,y), and NR is the total number of readouts of the array since the last reset. In the corners of a full 26-readout MULTIACCUM response there will be of order 500-800 DN due to amplifier glow, as well as the associated Poisson noise from this signal. Because amplifier glow is a radiation source detected by the array, it is subject to the non-linearity and DQE characteristics of the array. The low-level non-linearity has not yet been well characterized, leaving some uncertainty in the correction. One standing problem for the characterization of the glow non-linearity is the unknown source signal in the science data images, since this is signal added to the amplifier glow signal and therefore contributes to the non-linear behavior. In many cases, the non-linearity is expected to induce small uncertainties in the final calibrated data.
Shading
Shading is a noiseless signal gradient, a pixel-dependent bias, orthogonal to the direction of primary clocking. The shading effectively changes the bias level for the pixels as a function of time and also of location, because the first pixels to be read show the largest bias change. Visually, this appears as a ripple and a signal gradient across a given quadrant of an uncorrected image. The amplitude of the shading can be as large as several hundred electrons for some pixels under some circumstances. The shading exhibits all the characteristics of a bias change, including lack of noise (within our measurement uncertainties). Through analysis of on-orbit dark data, we have determined that for a given pixel the bias level superimposed on the signal by the shading is dependent on the time since the last read (not reset) of the pixel. Thus if the time  t between reads remains constant, the bias level introduced by the shading remains constant. For MULTIACCUM readout sequences where the time between readouts is increasing logarithmically, the bias level changes with each successive read, and thus the overall shading pattern evolves with readout. The functional form of the shading is nearly exponential with
t between reads remains constant, the bias level introduced by the shading remains constant. For MULTIACCUM readout sequences where the time between readouts is increasing logarithmically, the bias level changes with each successive read, and thus the overall shading pattern evolves with readout. The functional form of the shading is nearly exponential with  t and quite repeatable, although there are some circumstances when repeatability is not exact (namely, on orbit testing of the MIF sequences has shown that changing from a very long
t and quite repeatable, although there are some circumstances when repeatability is not exact (namely, on orbit testing of the MIF sequences has shown that changing from a very long  t to a very short one introduces non-linearities in the functional form of the shading).
t to a very short one introduces non-linearities in the functional form of the shading).
Although a numerical fit to the shading function is possible in principle, we have chosen to generate bias images for each of the  t of each of the MULTIACCUM sequences from on-orbit data. In building a synthetic dark, the appropriate bias image:
t of each of the MULTIACCUM sequences from on-orbit data. In building a synthetic dark, the appropriate bias image: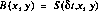
where B(x,y) is a function of the pixel location, can then be added to the other two components.
Making a Synthetic Dark
The total dark signal in any given pixel of any given NICMOS MULTIACCUM readout is just the sum of the three components above: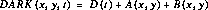
17.2.3 Uncertainties in the Synthetic Darks
The uncertainties in the dark frames described in this section are preliminary and will evolve as more on-orbit dark frames are obtained. Two types of uncertainties, random and systematic, can be identified in the synthetic darks.
Random Uncertainties
In the center of the NICMOS arrays, where the effects of shading and amplifier glow are smallest, the noise in the synthetic darks have uncertainties dominated by the readout noise. Because typically 15 measurements or so are used per read per pixel, the estimated uncertainities are of the order of 1 DN (about 5 electrons). In the corners of the arrays the amplifier glow is the largest source of noise, increasing as a function of the number of readouts. For the largest number of readouts (26) the estimated uncertainty is of the order of 5 DN (about 27 electrons). The random uncertainties in the dark frames are thus spatially dependent.
Systematic Uncertainties
Comparison of on-orbit to synthetic darks shows that the differences between the two are relatively small-on the order of 0 to 15 DN, with some excursions to 30-40 DN in the corners of the arrays for the final reads of full 26-readout sequences. Most of these differences are due to over- or under-subtraction of the amplifier glow. A better characterization of the amplifier glow from on-orbit data should alleviate these systematic effects.
The dark current pedestal adds some uncertainty to the synthetic darks, since on-orbit dark frames are used to generate synthetic darks. However, every effort was made to throw away pedestal-affected data when making the reference files currently in the database.
One standing problem is the proper shading correction in the second of the multiple readouts at the end of a MIF sequence. This single readout is the only one for which a shorter  t occurs after a longer one in any of the MULTIACCUM sequences. A different shading function is observed for this readout, lower by about 50-100 DN than expected for the specific
t occurs after a longer one in any of the MULTIACCUM sequences. A different shading function is observed for this readout, lower by about 50-100 DN than expected for the specific  t, and with a smooth gradient across a given quadrant in the readout direction. All previous and subsequent readouts appear unaffected by this problem. The effect of this one imperfect dark frame is typically rather small in the final calibrated image.
t, and with a smooth gradient across a given quadrant in the readout direction. All previous and subsequent readouts appear unaffected by this problem. The effect of this one imperfect dark frame is typically rather small in the final calibrated image.
[Top] [Prev] [Next] [Bottom]
stevens@stsci.edu
Copyright © 1997, Association of Universities for Research in Astronomy. All rights
reserved.
Last updated: 11/13/97 17:23:05