Breaking the Relational Taboo

Michael J. Kamfonas

The ability to represent dimensions as recursive hierarchies can be a valuable addition to the data warehouse designer's toolbox

As a data warehouse or data mart designer, it's inevitable that you'll encounter those few special dimensions that have too many levels or uneven branches. Or that may have complex segmentation rules you don't know at design time. You probably wish you didn't have to force-fit such dimensions into a rigid, fixed-depth hierarchy, but instead represent them as recursive hierarchies. In this article, I'll present a node enumeration method that lets you represent dimensions as recursive hierarchies without the disadvantages of recursive SQL. By encoding the dimension's hierarchical topology into a pair of integers attached to every node, we shift most of the costly work to a preparatory step executed after data maintenance that's similar to indexing. What's the advantage of this alternative? Transitive closure is reduced to a "between" predicate of a SQL query that executes a level of magnitude more efficiently than recursive SQL extensions.

Hierarchies and Dimensional Information Models

Society has used hierarchical decomposition for thousands of years to classify objects and artifacts, structure organizations, plan activities, and organize knowledge. Such structures are inevitably manifest in dimensional information models as product taxonomies, customer segmentations, and cost and account decompositions, to mention only a few. We will focus on such hierarchies with the following basic characteristics:

Their nodes participate in a binary relationship type (arcs), forming a tree graph. Each node has a maximum of one parent but potentially has many children. Different branches of the tree may have different depth. If your dimension has multiple roots, you can view those roots as a null parent's children, making a single tree with a null root.

The graph-defining binary relationship is a step relationship. Such a relationship is exemplified by "is parent of," "immediately reports to," or "is part of." Dimensions often have a classifying criterion (reporting, containment); however, you can use explicit hierarchies for arbitrary segmentation hierarchies, such as the ones classifying markets or customers. In such cases, classification rules vary from branch to branch and level to level.

"Transitive closure" refers to the set of generated transitive relationships. For example, you can define ancestor as either a parent or a parent's ancestor-- the same as defining ancestors as parents, parents of parents, parents of parents of parents, and so on. Similarly, you can define "reports to" as the relationship between any two organizations connected by a chain of "directly reports to" relationships. Finally, you can derive the "includes/is used in" relationship as a chain of "part of" relationships.

From now on, instead of abstract constructs, we'll adopt the organization and the reporting relationship to illustrate the concepts presented. The following relation identifies such an organizational entity:

org(TID, PID, NAME, other properties...)

TID is the "token ID" serving as the organization dimension's surrogate name. The PID is the "Parent ID," denoting a reference to the parent organization. Because this is a hierarchical structure, only one parent per node is possible. The highest level organizations will have no parent; the PID is either NULL or the default value. For the purposes of our example, we will use numeric TIDs and PIDs and NULL in the top node PIDs to denote "no parent." In OLAP queries, you filter the dimension by selecting all organizations reporting to a given organization directly or indirectly. This filtering operation is particularly useful if you combine it with other dimension filters and join it to a fact in one SQL statement. Figure 1 shows the direct reporting relationships.

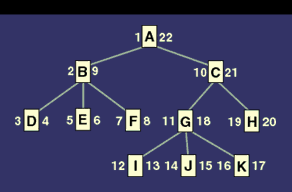
Figure 1 Tree graph with L and R Numbers

Let's say that you need to extract all unit expenses incurred under organization X. You'll either have to traverse the organizational structure for every such query, or prestore the table's transitive closure relationship. You can successfully traverse the structure using SQL extensions, such as the CONNECT BY clause in Oracle, or a recursive union of the DB2 family. You can also do this procedurally by reading X's successive layers of children, but you can't use such procedures as part of larger SQL queries.

The "prestored transitive closure" approach involves an intermediate table that contains X's descendents, and a join to the org table. The intermediate table is either temporary, generated every time you issue a query, or permanent, containing the transitive closure of the "reports to" relationship.

There are disadvantages to each of these solutions. The first actually "walks the structure," requiring multiple requests that let you extract children sets for each node you retrieve. The advantage of this approach is that it doesn't introduce any update anomalies because you don't maintain redundant data. The second solution uses set processing, but it requires that you maintain a very large redundant table and deal with the associated update anomalies. For example, a tree five layers deep with a fan-out of 10 children per node has a total of 11,111 nodes and 11,110 parent-child relationships. But there are more than 11,000,000 ancestor-descendent relationships in the transitive closure. A single maintenance operation may affect more than one million of these ancestor-descendent relationships. The cost of this approach grows geometrically as the fanout and depth grow. This option is undesirable only because of maintenance complications and the lack of scalability.

The L and R Design Approach

Observe the tree in Figure 1. The nodes represent org entities, and the arcs denote an "immediately reports to" relationship. Can you see how the two numbers on the left and right of each node can be used to identify all ancestor-descendant relationships? Any node's numbers lie between each of its ancestor's left and right numbers. In addition, a node's two numbers define the outside boundaries of all their descendants' numbers.

Let's call these two numbers L and R for the left and right one, respectively. These attributes encode the organizational entity's complete hierarchical ordering so you can use them in set queries. The following rules govern their use:

L and R share a common domain of ordered values that we'll call a binary integer. Each value of the domain is used only once, either as an L or an R value, but never as both an L and an R value. For a given node, the L value is strictly less than the R value.
Although unique, you don't use L and R for external identification of any entity. We can arbitrarily reassign L and R to facilitate efficient retrieval or to accommodate additional nodes in the hierarchy, similar to the way you can reorganize tables and indexes.
Any two nodes satisfy the ancestor-descendent relationship when the descendent's L (or R) value is between the ancestor's L and R values:

(L_i < L_j < R_i) <=> i ancestor of j

(L_i < R_j < R_i) <=> i ancestor of j

All L and R values of nodes hierarchically subordinate to a given node are in its L - R range, and this property isn't satisfied by any node that isn't hierarchically subordinate. For example, if l and r are organization X's respective L and R values, all organizations that report to X directly or indirectly will have their L (and R) between l and r.

You can view the L and R numbers as intervals. Each parent's interval covers the sum of its children's intervals, which define a topological ordering over the nodes. Numbering the nodes of a tree depth-first and traversing the nodes from left to right result in assigning L and R values. The enumeration process visits each node twice coming once from the top and a second and last time from below. The process keeps a running counter that dispenses sequential values, and assigns the L value at the first visit and the R value at the second visit. By following a depth-first left-to-right path, we insure that the process visits all the descendants of a node between its first and second visit. Figure 1 shows this numbering sequence.

Listing 1 shows two queries and a view. Case 1 returns the ancestors, and Case 2 returns the node descendents named QNAME. The "from" clause contains two references to the ORG table. "A" is the correlation name for the "ancestor" role, and "D" for the "descendent" role. All queries use the same predicate to restrict the descendent nodes' L values to fall in the (A.L..A.R) range.

Case 1:  Query of organization ancestors of QNAME (reporting chain up)

select   A.NAME,   . . .
from     ORG  A, ORG   D
where    D.NAME = :QNAME and
   D.L between A.L  and A.R
   

Case2: Query returning set of all direct and indirect reports to node identified by :QNAME as of :QDATE:

select  D.NAME,  . . .
from    ORG  A, ORG   D
where   A.NAME = :QNAME and
   D.L  between A.L  and  A.R

Case 3:  View returning ANAMEs of ancestors of :descendents DNAME as of :QDATE;

create view  org_anc  (DNAME, ANAME, . . .) as
select     D.NAME, A.NAME   . . .
from    ORG   A, ORG D
where    D.L  between   A.L  and A.R

Listing 1. Tree Queries.

The view in Case 3 relates descendents and ancestors. You can use this view to find ancestors given a list of descendents, or to find descendents given a list of ancestors. If you display the contents of the view, you'll find the transitive closure table contents previously discussed. Instead of joining the transitive closure table, we'll use the "between" predicate captured in the view to do the filtering. Having faith in the optimizer, the DBMS will push selections through the view to develop a plan equivalent to Case 1 or 2.

You may ask: "Why don't we use a hierarchical keyword to achieve the same result?" For example, an IP address-like scheme enumerates the nodes of a tree as 1,1.1,1.2,1.3,1.1.1, and so on. The problem with this scheme is that you have to start all qualifications from the top. Otherwise, you'll have to scan the whole index or table. With the L and R enumeration however, you can anchor your search at any level, relate any node to any other one, and still employ matching index scans.

Performance of the L and R Method

Descendent-seeking queries, such as the one in Listing 1's Case 2, are the most common and the most efficient. The optimizer will use a matching index scan to find the qualifying D.L values that lie between the A.L and A.R constants. With this query plan, the cost of descendent- seeking queries is one sweep through the index reading in a number of contiguous pages proportional to the answer set's size. In ancestor-seeking queries, such as Listing 1's case 1, the between predicate restricts a constant, D.L, between the two columns A.L and A.R. A combined index on L (descending) and R (ascending) helps these ancestor searches. The best plan we can expect for these queries is a matching lookup of D.L on the combined index, and a scan to the end of the index using index only access. Consequently, the average cost for ancestor-seeking queries is half an index-only scan.

The L and R method has a level of magnitude performance advantage over any recursive SQL method, such as the SQL recursive union or Connect By clause. The node enumeration captures the nodes' topological ordering once, thus enabling transitive closure in one simple step, as opposed to multiple invocations. Detecting whether two nodes have an ancestor-descendent relationship normally requires the path traversal from one node to the other. Using the L and R numbers, however, you can test any two nodes using a simple between clause--without traversing the graph. Because the L and R method doesn't need to traverse the structure, more selective predicates may filter down the qualifying rows before applying the ancestor-descendent qualification. In recursive SQL, path traversal has to happen on unconstrained node sets, postponing highly filtering predicates until after the paths are traversed exhaustively.

L and R descendant selection subqueries scale well, even in MPP, share-nothing environments. The simple ancestor-descendent range test is partitionable and combined with other partitionable filtering predicates and achieves distributed dimension qualification. Recursive SQL requires multiple, directed invocations of the children-seeking query before applying other predicates. This approach pays for latency delay roughly proportional to the depth of the traversed tree.

Using L and R Dimensions in Star Joins

We will now extend the concept from isolated dimensions into fact joins with multiple dimensions. Let's extend the example with a fact table--one that captures financial data: cost(ORG, TYPE, PERIOD, AMT). It references the lowest-level, organizational node hierarchy, a type hierarchy and a time period hierarchy. The fact table also captures the period amount as a metric. For every period, organization, and type, we record a fact. The top of Listing 2 describes our schema. Next, we look at the definitions of ORG_TC and TYPE_TC views that capture the transitive closure for the organization (ORG) and cost type (TYPE) dimensions, respectively. These views contain the attributes for each ancestor and each descendent pair, prefixed with A and D, respectively.

Schema:
org      TID, PID, NAME, L, R, LEVEL...
type     TID, PID, NAME, L, R, CLASS, POSTING?
period  WK_END_DT, MONTH, YEAR
cost      ORG, TYPE, PERIOD, AMT

Transitive Closure Views:
create view  org_tc   (DTID,DNAME, ATID,ANAME, . . .) as
select   D.TID,D.NAME, A.TID, A.NAME   . . .
from    ORG   A, ORG   D
where  D.L  between A.L  and A.R

create view  type_tc  (DTID,DNAME, ATID,ANAME, ...) as
select   D.TID,D.NAME, A.TID, A.NAME   . . .
from    TYPE  A, TYPE   D
where   D.L  between   A.L  and A.R

Query using Views:
select     O.ANAME, T.ANAME,P.MONTH,sum(AMT)
from    ORG_TC  O, TYPE_TC T, PERIOD P, COST C
where    P.WK_END_DT between  1/1/1998 and 8/1/1998
  and   O.ALEVEL = 'DEPT' 
  and   T.DCLASS = 'LABOR' 
  and    T.ALEVEL = 'S'
  and   P.WK_END_DT = C.PERIOD
  and   T.TID = C.TYPE
  and   O.TID = C.ORG
group by   O.ANAME, T.ANAME, P.MONTH
order by   3,1,2

Query using nested SQL:
With 
ORG_TC  as (select  distinct   D.TID, A.NAME
               from    ORG   A, ORG   D
               where    D.L  between   A.L  and A.R
               and   A.LEVEL = 'DEPT' ),
TYPE_TC as (select  distinct   D.TID,A.NAME
             from    TYPE  A, TYPE   D
             where    D.L  between   A.L  and A.R
               and   D.CLASS = 'LABOR' 
               and    A.LEVEL = 'S')
select     O.NAME, T.NAME,P.MONTH,sum(AMT)
from    ORG_TC  O, TYPE_TC T, PERIOD P, COST C
where    P.WK_END_DT between  1/1/1998 and 8/1/1998
   and   P.WK_END_DT = C.PERIOD
   and   T.TID = C.TYPE
   and   O.TID = C.ORG
group by   O. NAME, T. NAME, P.MONTH
order by   3,1,2

Listing 2. Dimensions in Context

Let's assume that we're seeking all labor charges grouped by month, at the organization's summary cost type level (TYPE.LEVEL = 'S') and department level. Listing 2 shows two query forms. The first one uses the transitive closure views, while the second exploits nested SQL and the SQL3 WITH clause. The first implementation is appropriate for any DBMS with an optimizer avoiding unnecessary view materialization, such as Oracle. The DB2 family supports either form; with slight modification, we can use temporary intermediate tables to implement the second form in Sybase.

You may have to deal with one complication: Dimension selections contain no duplicates during the join to the fact table. You can often guarantee this from the selection criteria alone. However, in cases in which you provide lists of ancestors with one being descendent of the other's, you may end up selecting the same descendent multiple times. Listing 2's nested SQL example uses the DISTINCT keyword in dimension subselects to guarantee duplicate elimination.

Generating L and R numbers

We saw how to exploit the L and R numbers for efficient, ancestor-descendant queries. Now we will focus on how to maintain these values. You may choose to incrementally update them as the table is changed; however, it is usually simpler to reassign them after table maintenance. Listing 3 shows an algorithm that assigns these numbers. The algorithm uses the parent-child relationship to walk the hierarchy from the root, depth-first, left-to-right. It assigns values to L and R using a simple counter. In order to let you insert new branches without having to re-enumerate all the nodes, we add a constant SKIP-VALUE prior to assigning the R value. You can subsequently use these gaps to fit L and R values when you add nodes to the hierarchy. The effect of skipping values in the enumeration sequence is similar to the effect that PERCENT_FREE has in an index. Online maintenance activities use the range of unused L and R values to attach or reallocate children. After a while, you fill these ranges and re-enumerate them using batch reassignment, an activity similar to that of index reorganization.

accept  constant SKIP; 
let  A:  array of {  TID:  primary key of org,
         L:     integer = 0,
         R: integer = 0}
   indexed by  i = 0;
initialize     integer: Counter = 0 ;

 load root nodes using
   select    TID, 0, 0
   from     ORG
   where    PID is NULL ;
   load  each  into  A after incrementing i by 1

i is left pointing to the last element loaded

while  i > 0 do   process last node of array until empty:
if  A[i].L  =  0 
   set A[i].L :=  ++ Counter
   append children of A[i].TID to A using
      select    TID, 0. 0
      from      ORG
      where  PID =  A[i].TID
      load each  into A after incrementing i by 1

           i  is left pointing to last element loaded
else
   set A[i].R :=  Counter + SKIP
   update  ORG[TIDi]   using
        update  ORG 
        set     L   = A[i].L
                 R = A[i].R
       where  TID = A[i].TID
   decrement  i  by  1
endif
repeat;

Listing 3. L and R Generation Algorithm

The algorithm starts by reading all nodes that don't have a parent and stores them in an array. The while loop processes the last array element by assigning the next L value from an incremented counter, and then appends all its children to the array. The while loop iterates, similarly assigning L values and appending the children of the last element it finds on the array until the last element is a node with no children. The array now contains concatenated consecutive children sets along one path of nodes defined by the lexicographically highest keys of each level.

In its next iteration, the while loop, still pointing at the last element, will execute the "else" side of the "if" statement, because the L value will now be nonzero. This code block assigns the R number of the childless element after incrementing the counter by the constant SKIP value. The code block updates the database and continues processing with the next item on the left in the array being the last element. If the while loop finds an unassigned L value that's a member of the same child set and follows the "if" section of code, the loop assigns an L value, appends its children, and so on. If, on the other hand, an L value is already assigned, all of this node's children are processed and stored in prior iterations. The "else" section of the code assigns the R and writes the node to the database before proceeding with the next node on the left.

Every time you enter the while loop, the following assertions are always true:

All node ancestors that aren't assigned an R value are between the beginning of the array and that node.
If an array node is assigned an L number, all its ancestors are assigned smaller L values.
If A[i] has an L number assigned, it has no children, or its children have been updated with L values higher than A[i].L and lower than or equal to the current counter value. Also, all L number ancestors are assigned smaller L values, and none has been assigned an R value.

The process continues until no nodes are left unprocessed on the array. The array size you need is equal to the maximum combined size of all children sets along any one path from any top to any leaf node.

The algorithm uses the array as a stack to process the tree in layers. It reads and updates each node once. Consequently, the algorithm's cost is of the order of the number of nodes in the tree.

You can improve the performance of this algorithm by avoiding the attempts to retrieve children from leaf nodes. You will have to mark all leaf nodes up front using a "Lowest Level" indicator. You can assign the appropriate value to the Lowest Level (LL) indicator as part of the initialization step of the algorithm, using two set update operations:

Update ORG set LL = Y;

Update ORG set LL = N where ORG.TID not used as a PID

The first update initializes all LL indicators, while the second marks all TIDs used as Parent IDs. By enhancing the while clause to use the LL value, you can avoid making unproductive attempts to extract children from nodes whose LL value is Y. The enhancement costs two table scans; you can justify this cost if the leaf node number is significantly larger than the nonleaf ones.

A word of caution: This algorithm assumes that the PID references do not form cyclic paths. If inserting or updating the table and the PID value guarantee the purity of the tree, the algorithm will be adequate. Otherwise, you need to add an "occurs check" to ensure that every time you read a new layer of children into the array A, none of these children will appear in their respective ancestors' paths.

Recursive or Fixed Hierarchies?

Recursive hierarchies are a valid alternative to fixed depth hierarchies. We have shown the "L and R Enumeration" design technique to represent dimensions or other complex hierarchies as recursive structures, and make transitive closure (ancestor-descendent) queries nearly as efficient as with fixed hierarchies. We have also delved into exploiting various SQL idioms and views to hide the complexities of the between join in implementing such queries. We also showed how you can maintain the L and R values needed to make the technique work.

When should you prefer recursive hierarchies over fixed ones? There are three motivations for leaving the security and simplicity of fixed hierarchy designs to pursue recursive designs:

The hierarchy has unknown or uneven depth, or it has too many levels
The hierarchy is based on complex, context-dependent segmentation rules, and you use practitioners to filter and group along an explicit structure, such as WBS and Market Segmentation hierarchies
You need to maintain aggregations at artificial nodes optimally chosen for sharing, but slightly under the usual querying levels. Not all levels of all branches need to be exposed to the users using a recursive hierarchy.

I am not proposing recursive hierarchies as a general substitute for all fixed-level dimensions or hierarchies. It's simpler to implement, maintain, and query fixed-depth dimensions. However, in some cases, you can cause unnecessary problems by forcing a dimension to a fixed uniform number of levels. The L and R enumeration technique offers performance advantages that make recursive hierarchies more plausible as a tool in your data warehouse or data mart design than most of the literature assumes.

Recursive hierarchies are desirable because they're flexible and are less of a performance concern. But keep in mind that they introduce a degree of complexity. Make sure that your front-end tools generate the proper SQL and that you work out a way to maintain them. Validate performance expectations using realistic size dimension and fact tables with respect to your DBMS and optimizer.

Recursive hierarchies can also implement slowly changing recursive dimensions using versioning or Ralph Kimball's "Type 2" design. The result is a very powerful, general dimension archetype.

Michael Kamfonas is chief architect and director of data warehouse technology for Lockheed Martin's Integrated Business Solutions, based in Valley Forge, Pa. In the past 12 years he designed multimillion dollar solutions for Fortune 500 businesses and government in diverse technology environments. You can email Michael at michael.kamfonas@lmco.com.

search - home - archives - contacts - site index