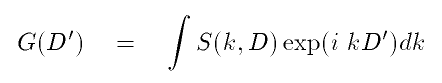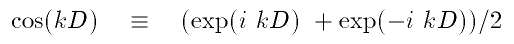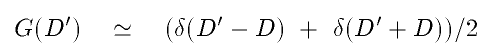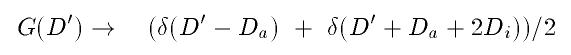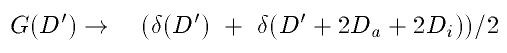We know that our measurement of F(k)V(k) is modulated by a cosine function and we begin by looking at the wavenumber dependence of S. If F(k)V(k) doesn't vary too rapidly with k then most of the variation of S is caused by the cos(kD+Φ) term. (For the moment, D=Da, i.e. we ignore the instrumental delay.) If we take a Fourier Transform of S with respect to k we should get a peak of the square modulus near D (the group delay), actually near +/- D. Once we know D we know cos(kD) and we can extimate FV. In practice we want to do this for a variety of D values so that we are not dividing by 0 at some values of k.
While it would be possible to use for D the phase delay, i.e. the visibility phase times
the mean wavenumber of its bandpass, the group delay method
has the advantage that it uses all the measured values of S(k) at one
instant to estimate D, which lowers the noise in this estimate. Another advantage, if
our spectral resolution is good, is that we don't have to keep D near the zero OPD, point,
i.e. the quality of the on-line fringe tracking is not very critical. In practise we
still modulate D a lot to both modulate most of the GARBAGE to supressed frequencies,
and to distinguish between the correct D and the image delay -D. If we change D in a known
way with the MIDI piezos, the correct peak of the delay function moves in the right direction.
Now representing the total OPD D as the sum of a known instrumental delay Di and
an unknown, but more slowly varying atmospheric component Da, we write the Fourier transform
of our signal S with respect to the wavenumber k as follows.
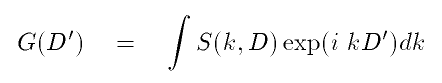
The square modulus of the function G(D') needs to be maximized, giving
the group delay. Here we show that this function has two symmetrical peaks, if we
set S(k)=cos(kD), and remember that
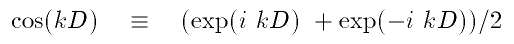
giving
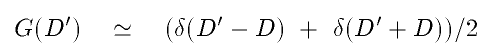
In reality, G(D') is of course not a delta-function but is convolved with the
Fourier-transform of B(k)V(k).
Since our unknown FK is modulated both at high frequency with the variation of Di
as well as at low frequency with the variation of Da, giving S, we multiply, for
the purpose of demodulation, S with first exp(-i kDi) which will change G(D)
to read
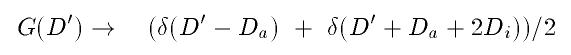
Di varies quickly and will be suppressed if we average. More accurately, what we have
done is to multiply our signal with the basis function of the FT, and by summing over all samples
of a fringe we have determined the complex FT of the signal at the modulation frequency. Second, we estimate
Da by averaging together the FTs of several
(almost coherent) scans, and finding the peak in the absolute
value of G(D'). This is called group delay determination.
Thus we multiply S by exp(-i kDa) so
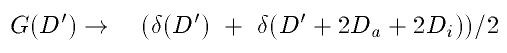
If we have done this correctly, the residual value of S remaining is
Note thate we have recovered the source phase Φ(k) except that any
component of Φ that is linear in k will have been removed when we fitted
the delay D. All valid individual measurements of S' can now be averaged together
to estimate F(k)V(k)