Display relative astrometry and fit an orbit
This type of astrometry is the measurement of relative positions in a binary
(or multiple) stellar system. Observations can be interferometric, speckle,
or even visual. The result are entered in a .psn file, as follows.
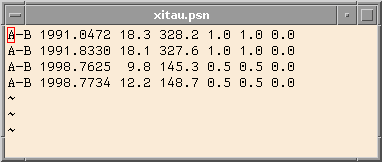
The columns have the component designation (obviously binary components),
the Julian Year, separation (mas) and position angle (deg from N), major and
minor semi-axis of the error ellipse and its position angle.
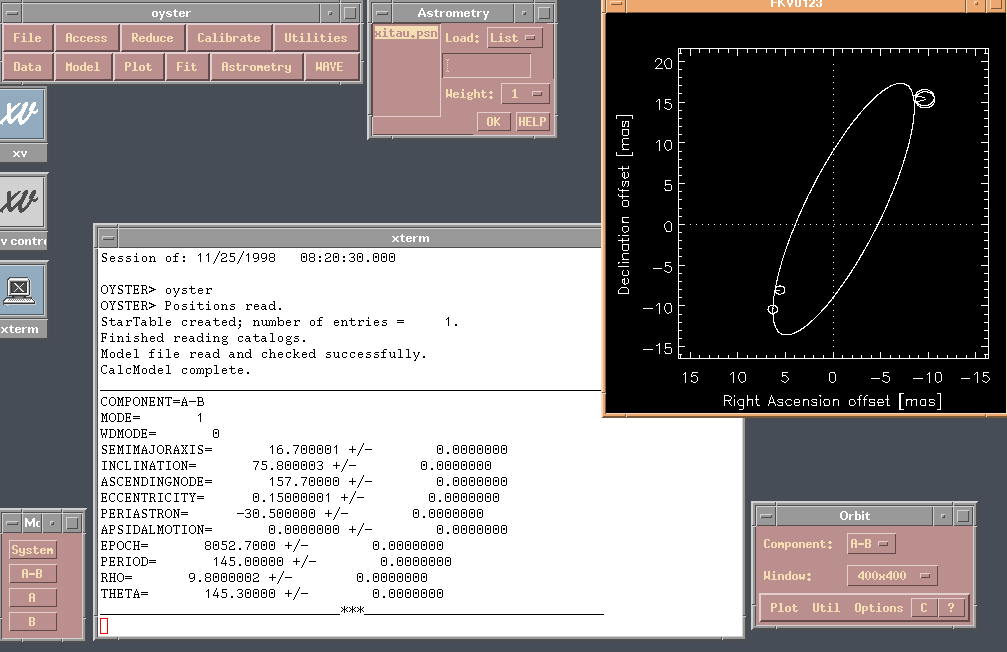
To plot the data (and model, here xitau.model), I have read the model,
computed the model values for the ASTROMETRY, and used Plot|ASTROMETRY
to produce the ASTROMETRY plot widget. Choose Option|Orbit and Error, and
this is what you will get.
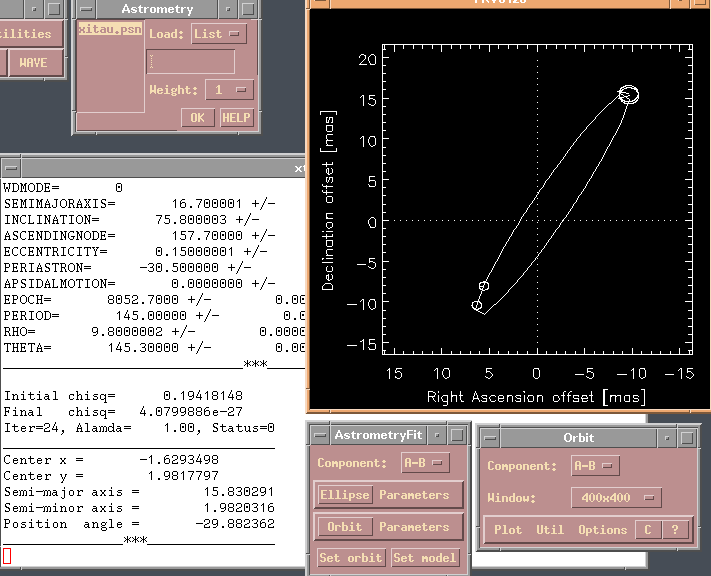
Let's assume you don't have a model, what are the steps to derive one? First,
plot the data and with Util|Ellipse and the mouse buttons interactively
define an apparent ellipse to fit your data as best as you can. Don't try
too hard, because you will improve the fit using Fit|ASTROMETRY. Select all
ellipse parameters and click on Fit. The following figure demonstrates the
procedure.
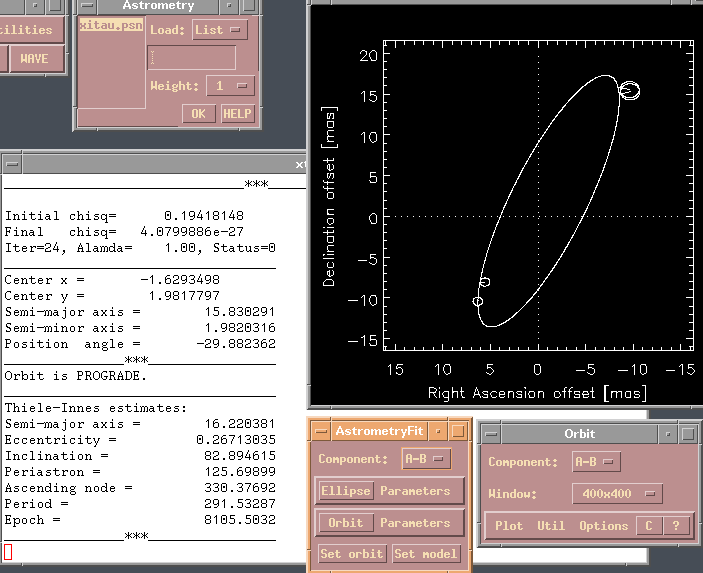
When you re-plot the data, it will show you the fitted ellipse. Now for a real
treat. Under Util|Orbit, there is a Thiele-Innes procedure to estimate the
orbital elements using your apparent ellipse and Kepler's laws! The results
are shown here, with the orbit plotted (de-select Options|Ellipse, re-select
Options|Orbit).
To improve the orbital elements, again using a Marquardt-Levenberg non-linear
fit algorithm, use Fit|Orbit in the Fit widget already displayed. Once this
is done, click on SetModel to transfer the orbital elements into your
AMOEBA model (for this to work, you have to have a real or dummy model loaded,
so that the data structure is available).
Next stop
Back to tour page
Back to main help page



