Evidence collected from ice crystals gathered during halo displays suggests that a typical halo-producing crystal has a size of 0.1mm or so. Crystals much smaller than this can certainly exist but, when they are comparable to or less than a few times the wavelength of light, the simple reflective/refractive optical effects needed for clear halo production are rendered less distinct by the blurring effects of diffraction: recall the fuzzy, white fogbow produced in place of the rainbow by the tiny water droplets in mist or fog. [Include a box about diffraction? Mention the effect of Brownian motion on the orientation of small crystals.] Crystals much larger than a few tenths of a mm are optically well-capable of halo production but there is the question of how these larger, heavier crystals fall through the air and whether they can attain the stable orientations needed to make some of the more spectacular halo arcs.
This brings us to one of the most interesting aspects of atmospheric halos. How do crystals fall and what causes them to settle into particular orientations? When an object falls slowly enough, the air moving past it flows in a smooth, ordered way without the appearance of any turbulence in its wake. This is called 'laminar flow' and it is what aircraft designers attempt to achieve around a wing - even though it may be moving very fast. An ice crystal is not much like a wing but there are circumstances where it can be surrounded by such a laminar flow. For this to happen, the crystal must be small and light enough to fall slowly: in practice less than about 30 cm/s. The size at which this speed is reached for ice is about 0.1-0.2 mm, depending on shape (see box). Larger crystals fall faster and consequently generate a turbulent flow around them.
People who study the properties and behaviour of the atmosphere need to be able to estimate the rate of fall of small particles and droplets, ranging from volcanic dust and windborne sand and salt crystals to rain and mist droplets. Calculating the downwards force due to the Earth's gravity is easy, all you need to know are the density, rho (actually the density of the droplet minus the density of the air to account for buoyancy) and size of the particle, from which its mass can be calculated. The force is then just the mass: m times the acceleration due to gravity, g. These small particles will accelerate until the gravitational force is matched by the resistive force of the viscous air which depends on the velocity, v, the coefficient of viscosity, eta and the size of the particle. The English physicist, Sir George Stokes in 1851, developed a formula for resistive force experienced by small spherical particles of radius a. This gives the equation:
4/3 pi r^3 rho g = m g = 6 pi eta a v
so
v = 2/9 rho a^2 g / eta
To actually calculate this, we need to know the viscosity of air - which depends on its temperature. This can be looked up in reference books and, at -40 degrees centigrade (typical for ice clouds in the upper atmosphere), has the value of 150 micropoise (the cgs unit of dynamic viscosity). Then using the density of ice (0.9 gm/cm^3) and the acceleration due to gravity (981 cm/s/s), we get the following table.
| a (mm) | v (cm/s) | R_e |
|---|---|---|
| 0.001 | 0.01 | 7E-06 |
| 0.002 | 0.05 | 6E-05 |
| 0.005 | 0.33 | 9E-04 |
| 0.01 | 1.3 | 7E-03 |
| 0.02 | 5.2 | 0.06 |
| 0.05 | 33 | 0.90 |
| 0.1 | 131 | 7.2 |
| 0.2 | 522 | 57 | 0.5 | 3265 | 897 |
| 1 | 13062 | 7175 |
Caption: The terminal velocity v reached by ice particles (assumed to be spherical with radius a in this calculation) falling in the upper atmosphere at a temperature of -40 degrees centigrade. The third column gives the value of the 'Reynolds number' R_e associated with the flow around the sphere. When this number becomes much larger than one, the flow becomes turbulent and the assumptions made in this calculation break down. The last three rows, therefore, are marked in red. If we repeat this calculation for thin plate crystals instead of spheres, we can have somewhat larger crystals, say up to 0.2 mm diameter, falling in the non-turbulent regime.
The third column in the table gives the value of a dimensionless number (ie. a pure number with no units) associated with the flow of air around the sphere. This is called the 'Reynolds number' R_e and it is widely used to characterise flows in hydro- and aerodynamics. It was introduced by the English physicist and engineer, Osborne Reynolds (1842-1912) who was interested in the flow of liquids in pipes. Flows occuring with a similar value of R_e have a similar appearance in terms of their degree of turbulence or lack of it. Look at some old war films where model battleships are used to recreate naval battles. The fact that the models move through the water in such an obviously unrealistic way is a consequence of the very different Reynolds numbers (by a factor of around 10,000) for models and ships of such different scales moving in water. When deriving his formula, Stokes assumed that R_e is less than about 1 and that the resistance to the sphere is dominated by viscosity rather than the dynamical effects produced by the speed of motion of the drop. As the last three rows in the table show that R_e >> 1, we should not believe the velocity as it should be calculated in a different and more complicated way. If you want to experiment by calculating R_e for different situations, it is given by:
R_e = rho L v / eta
where rho is the density of the fluid (0.0012 g/cm^3 for air at sea level and 0.00041 g/cm^3 at the altitude of ice clouds) and L is the 'dimension' of the object moving through it (L = 2 a for the sphere). For water at room temperature, eta = 10 millipoise (ie, about 60 times larger than that of air at the same temperature)
Using this expression for R_e, see if you can think of a way of making a realistic scaled-up model of a falling ice crystal. It is not so easy! What is the value of R_e for a falling leaf (a leaf has a density of about 1/2 that of water)?
Let's consider a plate-like crystal falling through the air (see figure). It may be easier to follow the argument by imagining the air flowing past a stationary crystal: it makes no difference to the physics. In an arbitrary orientation, the flow 'streamlines' are bent round the outer edges of the plate. The air following these distorted streamlines has to travel a little faster in order to keep up with its surroundings. Now faster moving air has a lower pressure than its slower neighbourhood. This is how an aeroplane wing develops 'lift' as explained by the theory developed by the Swiss physicist Daniel Bernoulli in 1738. The low pressure acts as a torque on the plate that tends to align it with its large face perpendicular to the flow. In other words, the plate will end up falling in a horizontal orientation. As soon as it tilts in some other direction the forces will become unbalanced due to the lowered pressure and act to move it back again. (R D Edge, 1976, Am J Phys, Vol 44, No 8, p780).
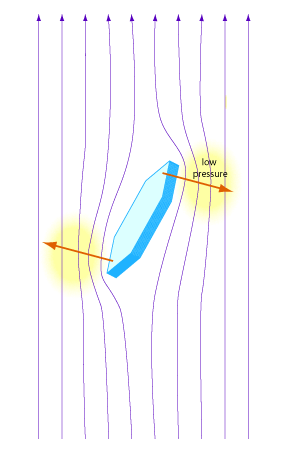
Caption: the flow of air past a plate crystal. The low pressure in the regions where the air speeds past the edge results in a torque that tends to align the plate across the flow.
A similar argument can be applied to a columnar crystal (one that is longer than it is across). The same forces will align such a crystal with its long axis horizontal. For columns with a regular hexagonal cross-section, there is little tendency to orient the crystal with any particular rotation angle around this long axis, but there are halo arcs produced by such crystals that are aligned with top and bottom faces horizontal. These are the so-called 'Parry arcs' and we shall discuss them later.
What happens to larger crystals that fall too fast and become surrounded by a turbulent flow? Well, this is hard to calculate but we can guess that they are less likely to be stable. Next autumn, have a look at some falling leaves. These all fall fast enough to generate turbulence and, while they tend to fall as slowly as they can by maximising their air resistance, they generally oscillate around the horizontal plane or even tumble around a long axis. We know that ice crystals oscillate by small angles as this makes the halo arcs fuzzier than we would expect if the crystals were always perfectly aligned. It is quite likely that the larger ones could oscillate by large angles or that plates could even tumble to produce the rarely seen 'Lowitz arcs'.
We have seen that the behaviour of ice crystals in the air is not so simple. Very small crystals will not produce distinct halos because diffraction effects will smear the reflected and refracted beams emerging from their faces. Large crystals will intercept and redirect a lot of light but, because of the complexities of aerodynamics, they may not settle into the special orientations needed to produce many of the more spectacular halo arcs. It seems that the optimum size for halo production is around a tenth or two of a mm. This is, indeed, a typical size of the wind-blown crystals collected during halo displays in the arctic regions (Tape). What are the sizes of crystals producing halos in high altitude cirrus? [can we get a reference to this?]
[Somewhere we need another section describing the formation of ice crystals in high altitude clouds at different temperatures and the origin of the wind-blown crystals responsible for some of the arctic displays. What do ice clouds look like? They have soft, indistinct edges since the crystals at the edge of the cloud, unlike water droplets, evaporate very slowly.]
Example of changing parhelion as a plane flies through turbulence