The overall image quality, in terms of angular image size and resolution, of an astronomical observation will be given by a quadratic sum of many different terms, among which the main ones are:
)
In order to guide the design of a telescope, a general error budget
tree is formulated. The organization of the error tree for
a modern telescope is shown in
fig. . It contains both manufacturing and
operation elements. The error budget is divided into two group:
on the one hand fixed errors due to manufacturing tolerances
and intrinsic limitations of the optical and mechanical
systems; on the other hand errors with short time
frequencies which depend on the variable conditions of the atmosphere.
This second group comprises natural seeing and the effects of local
turbulence (local seeing and wind).
The creation of an error budget among the various sources of error is often somewhat arbitrary for a complex system. In the case of a telescope an additional difficulty is given by the fact that fixed errors and tolerances should be added to terms of inherently variable nature that depend on the environmental conditions.
Figure: Structure of the error budget tree for the ESO VLT
The error budgets of telescope projects are traditionally given
in term of angular image size where the various
contributions
are
added quadratically.
Diericks has criticized this approach and proposed a new criterion for the evaluation of the effects of errors on the final image quality based on a parameter that he called Central Intensity Ratio (CIR) ([Diericks]), defined as
where S is the Strehl ratio of the telescope due to all effects:
optical aberrations, guiding errors, seeing, etc. and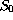 
is the
Strehl ratio of the equivalent perfect telescope (limited only by
diffraction) in the same natural seeing conditions.
Therefore the CIR covers all possible sources of errors including
local seeing effects with the
single exception of seeing of the free atmosphere. It must be noted
that the CIR is then a function of natural seeing, and it
improves for bad seeing conditions because the telescope errors become
more and more masked by the natural seeing.
One may note that
the CIR criterion has been proposed essentially because of its
convenience for defining without risk of over-specification the
polishing tolerances of the primary mirror. In this respect the
CIR is also more practical than the Strehl ratio, which for a large
telescope and poor seeing becomes extremely small
(cf. fig. ).
We will show in chapter of this report
that the CIR criterion is also a most suitable tool for
the objective evaluation of the disturbing influences of atmospheric
turbulence on the telescope performance.
For large ratios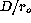 
and as long as it is 
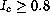, it can
be shown that the relation between the CIR, the FWHM angle
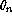due to the natural seeing and the telescope errors are:
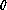is respectively the local seeing FWHM and/or the
rms slope error and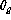 
is the rms guiding error.
Assuming that the individual errors are not correlated the decrease of CIR resulting from a combination of N different errors is simply the sum of the N individual CIR losses:
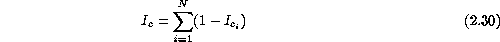
Fig. shows the error budget of the ESO VLT in
terms of the Central Intensity Ratio.
It is to be noted that
to date there are no established methodologies to verify the
performance of the wind and seeing dependent terms
in a manner that reflects the
actual operation of the telescope and as a consequence also the budget
values for these terms are generally set rather arbitrarily.
A contribution toward a solution to this problem will be given in
chapter .
Figure: Actual
image quality budget of the ESO VLT in terms of the
Central Intensity Ratio
