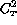 ,
which is defined in section
,
which is defined in section  .
We have also seen that the temperature structure coefficient is
related to the dissipation rates of kinetic energy and temperature:
.
We have also seen that the temperature structure coefficient is
related to the dissipation rates of kinetic energy and temperature:




The thermal turbulence which causes the effect of seeing can
quantified by the local temperature structure coefficient 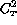 ,
which is defined in section
,
which is defined in section  .
We have also seen that the temperature structure coefficient is
related to the dissipation rates of kinetic energy and temperature:
.
We have also seen that the temperature structure coefficient is
related to the dissipation rates of kinetic energy and temperature:
where 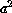 is a constant equal to about 3.
is a constant equal to about 3.
Introducing the eddy coefficients 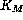 for momentum and
for momentum and 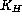 for
temperature, the respective dissipation rates can be expressed
in tensor notation as:
for
temperature, the respective dissipation rates can be expressed
in tensor notation as:
The last term at the right side accounts for buoyancy effects.
If the mean characteristics generally depend only on one geometrical
coordinate, as it is the case in a stationary atmospheric boundary
layer with the
height z above the ground, the above expressions become:
[Wyngaard] has analyzed in detailed, on the basis of
experimental data, the parameterisation of 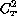 in terms of the
temperature and velocity fields in the atmospheric surface layer using
the so-called similarity theory.
in terms of the
temperature and velocity fields in the atmospheric surface layer using
the so-called similarity theory.
Similarity theory is a method by which statistical mean and turbulent values in a flow/temperature field, when properly adimensionalized, are assumed to be universal constant or functions of a stability parameter. The adimensionalizing quantities, called scaling variables, and the stability parameter can be chosen in different ways by obeying to some simple rules (see for instance [Hull], pp. 347-361).
Here the scaling variables taken are the height z and the temperature
gradient 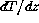 , while the Richardson number was used for
the stability parameter:
, while the Richardson number was used for
the stability parameter:

Noting that similarity theory predicts that 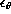 and
and
 , hence
, hence
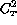 , when adimensionalized are universal function of Ri,
[Wyngaard] derived the expression
, when adimensionalized are universal function of Ri,
[Wyngaard] derived the expression
The function f(Ri), obtained from experimental measurements
is plotted in fig.  and
is a good illustration of the fundamental asymmetry of thermal
turbulence, hence seeing, with respect to the sign of the temperature
gradient.
As a numerical exercise we have computed
and
is a good illustration of the fundamental asymmetry of thermal
turbulence, hence seeing, with respect to the sign of the temperature
gradient.
As a numerical exercise we have computed 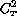 by means of
expression (
by means of
expression ( ) as a function of
) as a function of  for three different speed rms
for three different speed rms 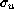 values at 15 meters
height above the ground (fig.
values at 15 meters
height above the ground (fig.  ).
One will note that
the effect of even small variations of
).
One will note that
the effect of even small variations of 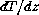 on
the local
on
the local 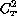 is very significant. The achievement of low seeing
implies very small temperature gradients, particularly in unstable
conditions.
An exception is given by the case of a stable gradient with low
mechanical turbulence. This is possibly the plainest demonstration
that quiet inversion layers have very favorable seeing
characteristics.
is very significant. The achievement of low seeing
implies very small temperature gradients, particularly in unstable
conditions.
An exception is given by the case of a stable gradient with low
mechanical turbulence. This is possibly the plainest demonstration
that quiet inversion layers have very favorable seeing
characteristics.
The variations of mechanical turbulence have opposite effects on

depending if the thermal conditions are unstable or stable.
For unstable conditions and a same 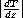 ,
,
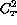 decreases with increasing turbulence.
For stable conditions
decreases with increasing turbulence.
For stable conditions 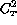
increases dramatically with increasing turbulence. This means for instance that the artificial inversion obtained by chilling the dome floor in some observatories (CFHT, ESO 2.2-m) does achieve a low seeing only as long as no wind turbulence enters the dome.

Figure: The function f(Ri)
in equation (5.7) - from [Wyngaard]

Figure: Computation of  versus
versus 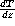 in the
atmospheric surface layer, 15 m above the ground
in the
atmospheric surface layer, 15 m above the ground
By choosing other scaling variables, namely the friction velocity
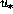 and the surface heat flux q (in K m s
and the surface heat flux q (in K m s ), and as the
stability
parameter the ratio
), and as the
stability
parameter the ratio 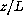 , where L is the Monin-Obukhov length
, where L is the Monin-Obukhov length

[Wyngaard] obtains another expression for 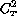 :
:
where 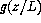 is an empirical function evaluated from
experimental data as:
is an empirical function evaluated from
experimental data as:
In presence of
a strong turbulent flow, L is large and therefore
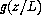 close to the surface
is constant
close to the surface
is constant 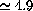 and equation (
and equation ( ) becomes:
) becomes:
We note that this expression may be derived also directly from
the general expression ( ).
When friction effects predominate over buoyancy
the second term of equation (
).
When friction effects predominate over buoyancy
the second term of equation ( ) may be neglected.
Putting
) may be neglected.
Putting 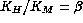 we obtain:
we obtain:
With this approximation and using a common parameterisation for the K factors:
where k is the Von Karman constant (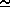 0.4),
0.4),
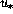 is the friction velocity,
is the friction velocity, 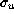 the velocity rms
and q the vertical heat flux,
expression (
the velocity rms
and q the vertical heat flux,
expression ( ) can be elaborated as
) can be elaborated as
Near the surface the heat flux q is practically equal to the surface
flux 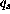 , which in a turbulent surface layer is
proportional to
, which in a turbulent surface layer is
proportional to 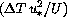 .
.
Therefore in a turbulent near-neutral surface layer
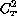 is proportional to
is proportional to 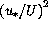 hence
to
hence
to 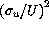 which is the square of turbulence intensity
which is the square of turbulence intensity 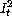 .
One then finds that
.
One then finds that 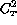 is directly related to both the squares of
turbulence intensity and temperature difference:
is directly related to both the squares of
turbulence intensity and temperature difference:
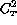 can also be put in relation with the outer scale of turbulence
can also be put in relation with the outer scale of turbulence
 . Following [Tatarskii], the outer scale of turbulence is related
to
. Following [Tatarskii], the outer scale of turbulence is related
to 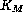 as
as

inserting this expression into ( ) we obtain
) we obtain
The free convection case
When the flow is strongly unstable, that is when, approaching the free
convection condition, buoyancy predominates over
friction effects such that 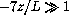 ,
expression (
,
expression ( ) becomes
) becomes
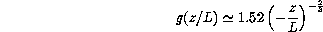
inserting in equation ( )and using the definition of L,
one obtains an expression in which
)and using the definition of L,
one obtains an expression in which 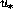 disappears:
disappears:
This relationship between surface flux, height and  is
graphically illustrated in fig.
is
graphically illustrated in fig.  below.
below.
Another expression for the free convection case can be obtained
quite simply from equation ( ), noting that the function
), noting that the function
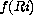 becomes about 3.6 for
becomes about 3.6 for 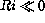 (cf. fig.
(cf. fig.  ):
):
which has the same form as equation ( ) and
where the distance z may be interpreted as a length scale parameter
which characterizes flow mixing in the free convection circulation
process.
) and
where the distance z may be interpreted as a length scale parameter
which characterizes flow mixing in the free convection circulation
process.
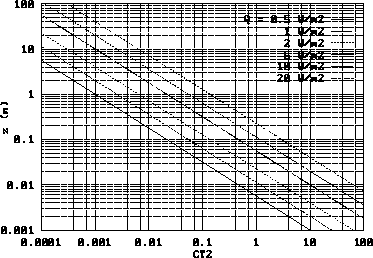
Figure: Relationship between 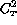 ,
height and surface
heat flux in free convection over a horizontal surface
,
height and surface
heat flux in free convection over a horizontal surface



