Let y(x,a) be a function where
![]() are the independent variables and
are the independent variables and
![]() are the p parameters lying in the domain A. If A is not the whole
space
are the p parameters lying in the domain A. If A is not the whole
space
![]() ,
the problem is said to be constrained.
,
the problem is said to be constrained.
If a situation can be observed by a set of events
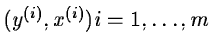 ,
i.e. a
set of couples representing the measured dependant and
variables, it is possible to deduce the value of the
parameters of your model y(x,a) corresponding to that situation.
As the measurements are generally given with some error, it is
impossible to get the exact value of the parameters but only an
estimation of them. Estimating is in some sense finding the most likely
value of the parameters. Much more events than parameters are in general
necessary.
,
i.e. a
set of couples representing the measured dependant and
variables, it is possible to deduce the value of the
parameters of your model y(x,a) corresponding to that situation.
As the measurements are generally given with some error, it is
impossible to get the exact value of the parameters but only an
estimation of them. Estimating is in some sense finding the most likely
value of the parameters. Much more events than parameters are in general
necessary.
In a linear problem, if the errors on the observations
have a gaussian distribution, the ``Maximum Likelihood Principle'' gives you
the ``best estimate'' of the parameters as the solution
of the so-called ``Least Squares Minimization'' that follows:
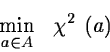
![\begin{displaymath}\chi^2~(a)~=~\sum_i~w^{(i)}~[~y^{(i)}~-~y(x^{(i)},a)~]^2~\end{displaymath}](img266.gif)
The quantities
If y(x,a) depends linearly on each parameter aj, the problem is also known as a Linear Regression and is solved in MIDAS by the command REGRESSION. This chapter deals with y(x,a) which have a non-linear dependance in a.
Let us now introduce some mathematical notations.
Let g(a) and H(a) be respectively the gradient and the Hessian
matrix of the function ![]() .
They can be expressed by
.
They can be expressed by
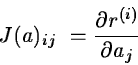
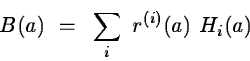
In the rest of the chapter, all the functions are supposed to be differentiable if they are applied the derivation operator even when this condition is not necessary for the convergence of the algorithm.
A certain number of numerical methods have been developed to solve the non-linear least squares problem, four have so far been implemented in MIDAS. A complete description of these algorithms can be found in [1] and [3], the present document will only give a basic introduction.