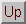



Next: The Corrected Gauss-Newton No
Up: Outline of the Available
Previous: The Modified Gauss-Newton Method.
This is identical to the modified Gauss-Newton method,
except in the way that the Hessian matrix is approximated.
This matrix is first initiated to zero.
At each iteration, a new estimation of the Hessian is
obtained by adding a rank one or two correction matrix to the last
estimate such that H(k+1), the estimate of the Hessian matrix at the
k+1th iteration, satisfies
(J(a(k+1))T J(a(k+1)) + H(k+1)) (x(k+1)-x(k)) = J(a(k+1)) r(a(k+1)) - J(a(k)) r(a(k))
The so-called BFGS updating formulas are applied in this algorithm
H(0) = 0 H(k+1) = H(k) + C(k)
where
W(k)=J(a(k+1))T J(a(k+1))+H(k)
and
y(k)=J(a(k+1))r(a(k+1))-J(a(k))r(a(k)) ,
please see Gill, Murray and Pitfield (1972) for more details.
After some iterations and around the optimum, H(k) converges to
the Hessian.
This method requires the knowledge of the derivatives and, as the
gradients are only computed once per iteration and consequently, the
Hessian is more roughly approximated than with the modified
Gauss-Newton method, this is better designed
for a great number of parameters i.e. p > 10.




Next: The Corrected Gauss-Newton No
Up: Outline of the Available
Previous: The Modified Gauss-Newton Method.
Petra Nass
1999-06-09