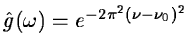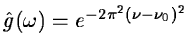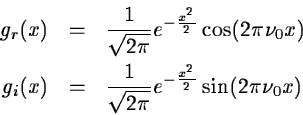Next: Mexican Hat
Up: Examples of Wavelets
Previous: Examples of Wavelets
The wavelet defined by Morlet is [16]:
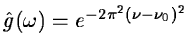 |
|
|
(14.7) |
it is a complex wavelet which can be decomposed in two parts, one for
the real part, and the other for the imaginary part.
where 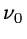 is a constant.
The admissibility condition is verified only if
is a constant.
The admissibility condition is verified only if
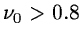 .
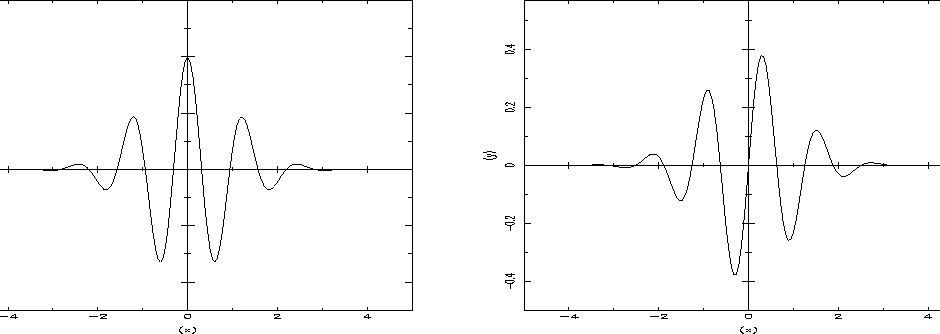
Figure 14.1 shows these two functions.
.
Figure 14.1 shows these two functions.
Figure 14.1:
Morlet's wavelet: real part at left and imaginary part at right.
 |
Petra Nass
1999-06-15