



Next: Hierarchical adaptive filtering
Up: Noise reduction from the
Previous: Hierarchical Wiener filtering
Adaptive filtering from the wavelet transform
In the preceding algorithm we have assumed the properties of the
signal and the noise to be stationary. The wavelet transform was first
used to obtain an algorithm which is faster than classical Wiener
Filtering. Then we took into account the correlation between two
different scales. In this way we got a filtering with stationary
properties. In fact, these hypotheses were too simple, because in
general the signal may not arise from a Gaussian stochastic
process. Knowing the noise distribution, we can determine the
statistically significant level at each scale of the measured wavelet
coefficients. If wi(x) is very weak, this level is not significant
and could be due to noise. Then the hypothesis that the value
Wi(x) is null is not forbidden. In the opposite case where
wi(x) is significant, we keep its value. If the noise is Gaussian,
we write:
| Wi = |
0 |
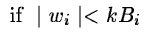 |
(14.90) |
| Wi = |
wi |
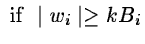 |
(14.91) |
Generally, we choose k = 3.
With a filter bank we have a biunivocity between the image and its
transform, so that the thresholded transform leads to only one restored
image. Some experiments show us that uncontrolled artifacts
appear for high level thresholding (k=3). The decimation done at
each step on the wavelet transform takes into account the
knowledge of the coefficients at further resolutions. The
thresholding sets to zero the intrinsic small terms which play their part in
the reconstruction. With the lattice filter the situation is very
different. No decimation is done and the thresholding keeps all
significant coefficients. Where the coefficients are set to zero, we
do not put zero, but we say that these values are unknown. The redundancy
is used to restore them. Before the thresholding we have a
redundant transform, which can be decimated, after the
thresholding we get a set of coefficients from which we wish to
restore in image.
If one applies the reconstruction algorithm, then it is not guaranteed
that the wavelet transform of the restored image will give the same
values for the coefficients. This is not important in the case where
they are not significant, but otherwise the same values must be
found. If W(s)i are the coefficients obtained by the
thresholding, then we require Wi(x) such that:
| P.Wi(x) = W(s)i(x) |
|
|
(14.92) |
where P is the non linear operator which performs the inverse
transform, the wavelet transform, and the thresholding. An
alternative is to use the following iterative solution which is
similar to Van Cittert's algorithm:
| W(n)i(x) = Wi(s)(x) + Wi(n-1)(x) - P.Wi(n-1)(x) |
|
|
(14.93) |
for the significant coefficients (
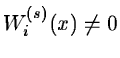 )
and:
)
and:
| Wi(n)(x) = Wi(n-1)(x) |
|
|
(14.94) |
for the non significant coefficients (
Wi(s)(x) = 0).
The algorithm is the following one:
- 1.
- Compute the wavelet transform of the data. We get wi.
- 2.
- Estimate the standard deviation of the noise B0 of the first plane
from the histogram of w0.
- 3.
- Estimate the standard deviation of the noise Bi from B0
at each scale.
- 4.
- Estimate the significant level at each scale, and threshold.
- 5.
- Initialize:
W(0)i(x) = Wi(s)(x)
- 6.
- Reconstruct the picture by using the iterative method.
The thresholding may introduce negative values in the resulting image.
A positivity constraint can be introduced in the iterative process,
by thresholding the restored image. The algorithm converges after
five or six iterations.




Next: Hierarchical adaptive filtering
Up: Noise reduction from the
Previous: Hierarchical Wiener filtering
Petra Nass
1999-06-15
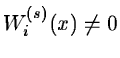 )
and:
)
and: