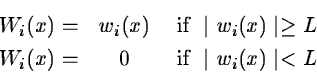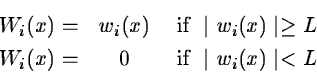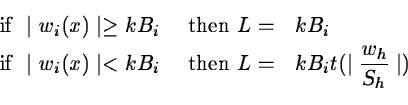Next: Comparison using a multiresolution
Up: Noise reduction from the
Previous: Adaptive filtering from the
Hierarchical adaptive filtering
In the previous algorithm we do not use the hierarchy of structures.
We have explored many approaches for introducing a non-linear
hierarchical law in the adaptive filtering and we found that the best
way was to link the threshold to the wavelet coefficient of the
previous plane wh. We get:
and L is a threshold estimated by:
where Sh is the standard deviation of wh. The function t(a)must return a value between 0 and 1. A possible function for t is:
- t(a) = 0 if
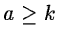
-
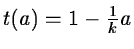 if a < k
if a < k
Petra Nass
1999-06-15