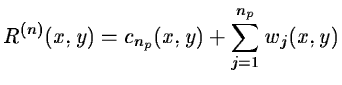Regularization from significant structures

If we use an iterative deconvolution algorithm, such as Van Cittert's or Lucy's one, we define R⁽ⁿ⁾(x,y), the error at iteration n:

R⁽ⁿ⁾(x,y) = I(x,y) - P(x,y) * O⁽ⁿ⁾(x,y) (14.111)

By using the à trous wavelet transform algorithm, R⁽ⁿ⁾ can be defined by the sum of its n_p wavelet planes and the last smooth plane (see equation 14.33).

 

$$R^{(n)}(x,y) = c_{n_p}(x,y) + \sum_{j=1}^{n_p} w_j(x,y)$$ (14.112)

The wavelet coefficients provide a mechanism to extract from the residuals at each iteration only the significant structures. A large part of these residuals are generally statistically non significant. The significant residual is:

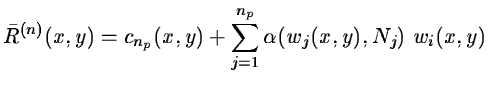$$\bar{R}^{(n)}(x,y) = c_{n_p}(x,y) + \sum_{j=1}^{n_p} \alpha(w_j(x,y), N_j) \ w_i(x,y)$$ (14.113)

N_j is the standard deviation of the noise at scale j, and $\alpha$ is a function which is defined by:

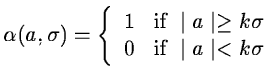$$\alpha(a, \sigma) = \left\{ \begin{array}{ll} 1 & \mbox{if } \mid a \mid \geq k\sigma \\ 0 & \mbox{if } \mid a \mid < k\sigma \end{array}\right.$$ (14.114)

The standard deviation of the noise N_j is estimated from the standard deviation of the noise in the image. This is done from the study of noise variation in the wavelet space, with the hypothesis of a white Gaussian noise.

We now show how the iterative deconvolution algorithms can be modified in order to take into account only the significant structure at each scale.