



Next: Regularization of the one-step
Up: Regularization from significant structures
Previous: Regularization from significant structures
Regularization of Van Cittert's algorithm
Van Cittert's iteration is:
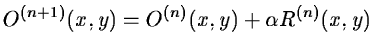 |
|
|
(14.115) |
with
R(n)(x,y) = I(x,y) - P(x,y) * O(n) (x,y).
The regularization by the significant structures leads to:
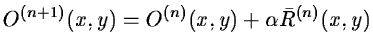 |
|
|
(14.116) |
The basic idea of our method consists of detecting, at each scale,
structures of a given size in the residual
R(n)(x,y) and putting
them in the restored image
O(n)(x,y). The process finishes when
no more structures are detected. Then, we have separated the image
I(x,y) into two images
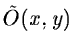 and R(x,y).
and R(x,y). 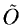 is
the restored image, which does not contain any noise, and R(x,y) is
the final residual which does not contain any structure. R is our
estimation of the noise N(x,y).
is
the restored image, which does not contain any noise, and R(x,y) is
the final residual which does not contain any structure. R is our
estimation of the noise N(x,y).
Petra Nass
1999-06-15
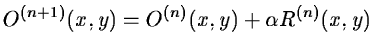
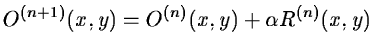
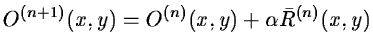
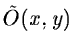 and R(x,y).
and R(x,y).