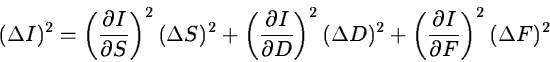 |
(18.7) |
The mean absolute error of INT_FRM(i,j) yields with ICONS = 1:
Computing the partial derivatives we get
This equation holds only at levels near the sky-background and is relevant
for detection of low-brightness emission. In practice however it is difficult
to get a similar exposure level for the FLAT_FRM and SCIE_FRM since the
flats are usually measured inside the Dome. From this point of view it is
desirable to measure the empty sky (adjacent to the object) just before or
after the object observations.