[Top] [Prev] [Next] [Bottom]
9.2 FGS Design
This section describes the Fine Guidance Sensor design, its optical train, the aperture, the S-curves that give the response of the instrument to positional changes, and the enhancements made to the refurbished FGS 1R, installed during the February 1997 servicing mission.
9.2.1 FGS Optics
An FGS is essentially a pair of two orthogonal white-light, equal-path interferometers, their associated optical and mechanical elements, and four photo-multiplier tubes (PMTs). Light from an object is collected by the telescope's primary mirror, reflected and focused by the secondary mirror, intercepted by a plane pickoff mirror before the focal point, and directed into the FGS and onto the Aspheric Collimating Mirror to produce a nearly collimated beam. The ray is directed to the optical elements of the Star Selector A (SSA) assembly. This rigid assembly of two mirrors and a five element corrector group can be commanded to rotate about HST's optical axis (V1). Two mirrors in the Star Selector A assembly deflect the beam and direct it through the five element corrector group that performs the final collimation and corrects for the optical aberrations induced by the aspheric mirror. They do not correct the spherical aberration arising from HST's mis-figured primary mirror.
The direction of the exit ray depends upon the incoming beam's angle of incidence on the SSA assembly, and therefore the rotation position of SSA and the beam's point of origin on the aspheric mirror which is, in turn, determined by the angle between the spacecraft's optical axis (V1) and the position of the star on the sky.
After exiting the SSA assembly the ray encounters a field stop to minimize scattered light and to narrow the field of view. The four mirrors of the Star Selector B (SSB) assembly receive the ray and redirect it through the filter wheel assembly and a plane fold flat mirror (FF3) reflects it onto the polarizing beam splitter. Like the SSA assembly, the SSB assembly can be commanded to rotate within HST's focal plane. Together the SSA and SSB assemblies transmit to the polarizing beam splitter only those photons originating from a narrowly defined direction, masking out all but a small (5" x 5") area of sky.
The polarizing beam splitter divides the incoming unpolarized light into two linearly plane polarized beams with orthogonal polarizations, each having roughly half the incident intensity, and directs them to the two Koesters prisms and their associated optics, field stops, and photomultiplier tubes (see Figure 9.1). Each of the two output rays from the polarizing beam splitter fall upon the face of the appropriate Koesters prism.
The Koesters prisms are constructed of two halves of fused silica joined together along a surface coated to act as a dielectric beam splitter. The dielectric performs an equal intensity division, introducing a 90 degree phase difference between the reflected and transmitted portions of the beam, with the transmitted lagging the reflected. This division gives the Koesters prism its interferometric properties because the beam reflected from one side of the prism, when joined with the transmitted beam from the other side, constructively or destructively interferes to a degree depending upon the angle between the incoming wavefront and the entrance face. Each Koesters prism thus emits two collimated exit beams whose relative intensities depend upon the tilt of the incident wavefront. Each beam is then focused and passed through a field stop to illuminate the surface of a photomultiplier tube (PMT) which records the number of photons received during each 25 msec interval.
The collimated beam entering each Koesters prism can be characterized by a propagation vector. The Koesters prism senses the tilt of this incident wavefront only in the direction perpendicular to the plane of the dielectric surface. Small rotations of the star selector A and B assembles can change the direction of the propagation vector, and hence the tilt of the incident wavefront at the face of the Koesters prism. When the component of the wavefront's propagation vector perpendicular to the plane of the dielectric surface is zero, a condition of interferometric null results, and the relative intensities of the two emergent beams, measured by the PMTs, will ideally be equal. Meanwhile, the other Koesters prism is sensitive to the wavefront's tilt in the orthogonal plane.
Figure 9.1 schematically displays the important optical and mechanical components of an FGS. Each Koesters prism is sensitive to the tilt of the wavefront about an axis which is parallel to the face of the prism and in the plane of the dielectric beam splitter (the shaded area within each prism).
Figure 9.1: The FGS Optical Train 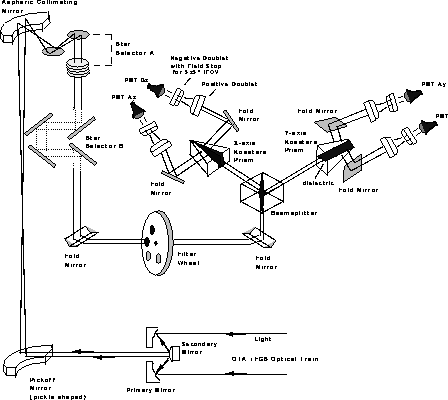
The fine sensitivity of the Koesters prisms to the angle of the incident radiation is what enables the FGS to measure star positions so accurately. For a star at a given position in FGS's detector space, there is a unique rotational position for each of the star selector A,B assemblies which brings that star's wavefront to zero tilt at the face of each Koesters prism. Therefore, the position of the star in the FGS detector space, and equivalently in HST's focal plane, can be measured precisely and accurately. Ultimately, the reliability of such measurements depends on the calibration of the instrument.
An (x,y) coordinate system maps the detector space of an FGS. The Koesters prisms are aligned such that one is sensitive to angular displacements along the x direction, the other along the y direction. Because each Koesters prism has two associated PMTs, each FGS has four PMTs in all. The two PMTs associated with the x-axis Koesters prism are labeled PMTXA and PMTXB. The other pair, associated with the y-axis Koesters prism, are labeled PMTYA and PMTYB.
 Note that the FGS (x,y) detector coordinate system differs from the POS TARG
coordinate system in the Phase II proposal instructions. The FGS coordinates
originate from the telescope's optical axis (V1 bore sight) while the POS TARG
system originates from the center of the detector's field of view. The POS TARG
system is used to convienently definte offsets.
Note that the FGS (x,y) detector coordinate system differs from the POS TARG
coordinate system in the Phase II proposal instructions. The FGS coordinates
originate from the telescope's optical axis (V1 bore sight) while the POS TARG
system originates from the center of the detector's field of view. The POS TARG
system is used to convienently definte offsets.
9.2.2 FGS Aperture
The instrument's total field of view (FOV), referred to as a pickle because it vaguely resembles the shape of a pickle, is a quarter annulus in the HST's focal plane, extending radially 10' to 14' from the telescope's boresight and axially 83.3° on the inner arc and 85° on its outer arc, an area of approximately 69 square arcminutes. The instantaneous field of view (IFOV) determined by the star selector assemblies and field stops is far smaller-5" by 5"-and its location within the pickle depends upon the Star Selector A and B rotation angles. Only those photons entering this IFOV aperture will be registered by the PMTs. To observe stars elsewhere, the star selector assemblies must be rotated to bring the IFOV to the target. This procedure is called slewing the IFOV.
The (x,y) location of the IFOV in the total FOV is determined from the rotation angles of the star selector A,B assemblies. Each FGS has its own detector space (x,y) coordinate system which maps into HST's (V1,V2,V3) coordinate system. FGS 2, and FGS 3 are nominally oriented at 90, and 180 degrees with respect to FGS 1, but small angular deviations are present. The FGS-to-FGS alignment matrix in the onboard flight software accounts for these deviations. Figure 9.2 and Figure 9.3 show the FGSs and their coordinate systems in the HST focal plane.
Figure 9.2: FGS Field of View (pickle) the HST Focal Plane with Local (x,y) Coordinate System Related to HST (V2,V3) System.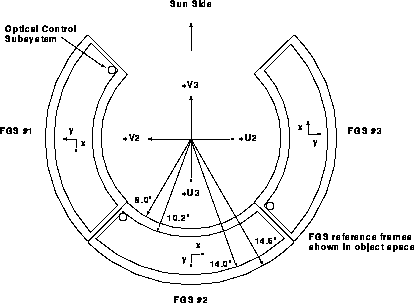
Figure 9.3: IFOV Placement in Pickle by Rotating SSA and SSB.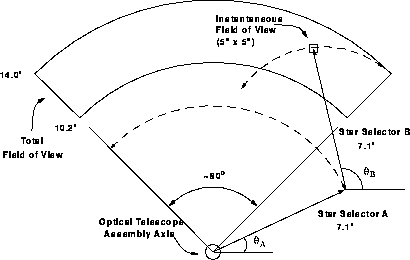
9.2.3 S-curves
As discussed earlier, each Koesters prism in an FGS is sensitive to the tilt of the incident wavefront in the direction perpendicular to the dielectric surface joining the two halves of the prism (see Figure 9.4, and Figure 9.5). Assuming the presence of a luminous point source in the IFOV, the relative intensity of the beams emerging from each Koesters prism is determined by the wavefront's tilt, and therefore responds to the rotations of the SSA and SSB assemblies that scan the IFOV across the star. The responses of the PMTs during such a scan provide the characteristic interferometric signature of the FGS. Graphing the normalized difference of the PMTs corresponding to a given channel against the position of the IFOV in detector space produces a figure known as an S-curve.
Figure 9.4: Emergent Beams from Koesters Prism and Photo-multiplier Tubes. The Koesters prism is sensitive to the tilt of the wavefront about an axis normal to the page and intersecting point B. 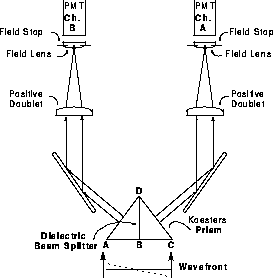
Figure 9.5 shows how a Koesters prism generates the characteristic S-curves shown in Figure 9.6. As the wavefront rotates about point B, the relative intensities of the two emergent beams change as a function of the tilt angle. If the tilt axis is not at point B, the beam is said to be decentered and the S-curve's morphology and modulation are degraded. Unfortunately, because HST's wavefront is spherically aberrated, a small decenter of the beam (0.5%) will cause 25% degradation of the S-curve's signal.
Figure 9.5: Internal Reflection and Transmission of the Beam Entering the Koesters Prism on the AC Face 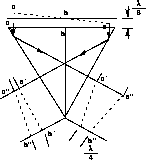
The Koesters prisms measure the two orthogonal wavefront directions and thus produces two S-curves, Sx and Sy. The x-axis S-curve is given by:
Sx = (Ax - Bx) / (Ax + Bx)
where Ax is the photon count from PMTXA (accumulated over 25msec), and Bx is the count from PMTXB. The y-axis S-curve is computed in a similar way. Figure 9.6 shows the S-curves for the x and y axes observed near the center of the field of view of FGS 3. When the IFOV is more than 100 mas from the location of interferometric null, the PMTs of a given channel record nearly equal intensities. But closer to the interferometric null a signal emerges as the Koesters prism produces beams of different relative intensities. The so-called zero point crossing between the +/- peaks of the S-curve ideally occurs at interferometric null. Note however, that the relative sensitivities of the PMTs and the optical paths traversed by the beam after emerging from the Koesters prism are not identical, and therefore, the zero point crossing may not occur exactly at the interferometric null. (This effect is accounted for in the data reduction process.) Because a one-to-one relationship exists between the rotation angles of the Star Selector A and Star Selector B assemblies and the x,y detector space coordinates, the values of these rotation angles at interferometric null can be used to measure the position of the star in x,y detector space.
Figure 9.6: FGS 3 S-Curves of Upgren69 in F583W at (x,y) = (0,0)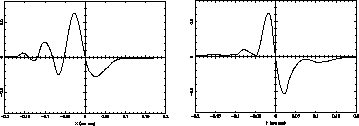
Field Dependencies of S-curves
S-curves can be measured anywhere in the FGS FOV. A standard star (UPGREN69) has been observed at nine standard positions within each of the three FGSs. The S-curves obtained from a given FGS are compared among themselves; any variation of the S-curve morphology (its shape) and modulation (its peak to peak amplitude) with position in the pickle is referred to as field dependency of the S-curve.
An FGS will display degraded S-curve performance when the collimated beam is not well centered on the face of the Koesters prism. In addition, given the presence of spherical aberration due to the misfigured primary mirror, the wavefront presented to the Koesters prism is not flat but has curvature, a fact that greatly amplifies the effects of optical misalignments. Specifically, a decentered beam in the presence of spherical aberration gives rise to coma and astigmatic aberrations, resulting in degraded S-curve characteristics.
The source of the field dependency is thought to be beam walk originating from a misalignment of the star selector B assembly with respect to the Koesters prism that changes as a function of SSB rotation angle. The Star Selectors center the beam on the face of the Koesters prisms while varying the tilt of the wavefront. If there is a clocking error in the alignment of SSB and the Koesters prism, the beam will not remain centered as SSB rotates, resulting in field dependency. Furthermore, if the amount of decentering changes with time, its effects must be monitored in order to calibrate the science data properly. The S-curve measurements in the original three FGSs indicated large decenters of the Koesters prisms in FGS 1 and FGS 2 and strong field dependency in FGS 3.
Figure 9.7 shows that the S-curves of FGS 1 and FGS 2 are not adequate for astrometric science. Only FGS 3 has S-curves with signal-to-noise ratios sufficient for precise astrometry.
 The face of the Koesters prism is 50 mm wide. In the presence of spherical aberration from the telescope's primary mirror, a decentering of the wavefront by only
0.25mm will decrease the modulation of the S-curve to 75% of its perfectly
aligned value. It has been determined that the decenters in FGS 3 range across the
pickle from +0.8 to -0.68 (mm) in x and +0.31 to -0.28 (mm) in y. If the telescope
were not spherically aberrated, mis-alignments up to 5 times this size would not
be noticeable.
The face of the Koesters prism is 50 mm wide. In the presence of spherical aberration from the telescope's primary mirror, a decentering of the wavefront by only
0.25mm will decrease the modulation of the S-curve to 75% of its perfectly
aligned value. It has been determined that the decenters in FGS 3 range across the
pickle from +0.8 to -0.68 (mm) in x and +0.31 to -0.28 (mm) in y. If the telescope
were not spherically aberrated, mis-alignments up to 5 times this size would not
be noticeable.
One way to minimize the effects of misalignment and the spherical aberration is to stop down the outer radius of the primary mirror of HST. All the FGSs have a 2/3 pupil stop on their filter wheels. This pupil stop retores the S-curves to a level which allows guiding across the entire pickle. Unfortunately, it also blocks 50% of the target's photons, so nearly a magnitude of sensitivity is lost. Figure 9.8 shows the improvement of the S-curve signature with the 2/3 pupil in place relative to the full aperture for the 3 FGSs at pickle center. Note also the performance of FGS 3 relative to FGS 1 and FGS 2 with full aperture.
Figure 9.7: Full-Aperture X and Y Axis S-curves of Original Three FGSs -Measured at the Center of Each FGS Field of View 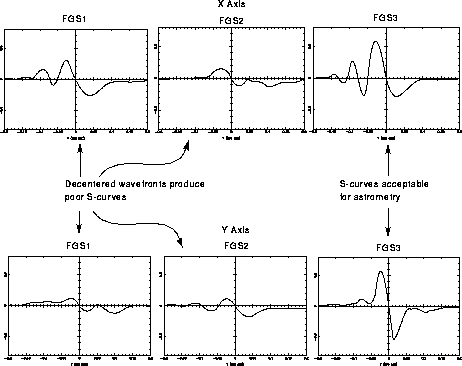
Figure 9.8: Dramatically Improved S-curves for FGS 1 and FGS 2 when Same Star is Observed through the 2/3 Pupil Stop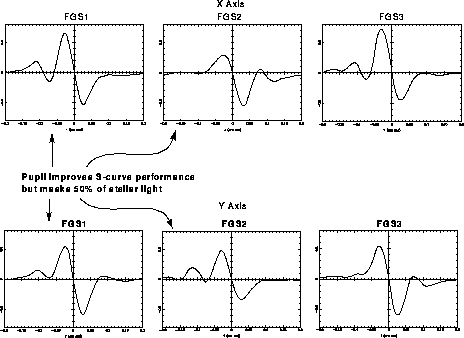
9.2.4 FGS 1R
The on-orbit evaluations of the FGSs in the presence of spherical aberration from the OTA has shown that proper alignment of the FGS's internal optics is absolutely essential to its performance. Moreover, the apparent decenters of the beams on the faces of the Koesters prisms for the 3 FGSs indicate that the pre-launch alignments within an FGS are not preserved once the instrument arrives in orbit. Therefore, Hughes Danbury Optical Systems, the manufacturer of the FGS, proposed that a refurbished FGS would greatly benefit from a commandable adjustment mechanism that recenters the beam at the Koesters prism. The replacement FGS in radial bay #1, installed on HST during the 1997 servicing mission and referred to as FGS 1R has such a mechanism. In essence one of the static plane fold flat mirrors (FF3) was replaced with an articulating mirror which can be commanded to place the output beam from the Star Selector B assembly at the centers of the two Koesters prisms. Unfortunately, this correction does not fix field dependency because any beam walk from SSB at the Koesters prism will remain. The FF3 mechanism can center the beam for only one SSB rotation angle.
The FF3 has been adjusted to yield near perfect S-curve performance at the center of FGS 1R's pickle. And although the S-curves of FGS 1R show field dependency, it is not as extreme as that in FGS 3. Therefore, with excellent S-curves at pickle center and improved performance (relative to FGS 3) everywhere else, FGS 1R is potentially the best astrometric science instrument onboard HST. Figure 9.9 and Figure 9.10 compare the S-curves from three positions in the pickle of FGS 3 with those from FGS 1R.
Figure 9.9: Field Dependency of FGS3 Across the Pickle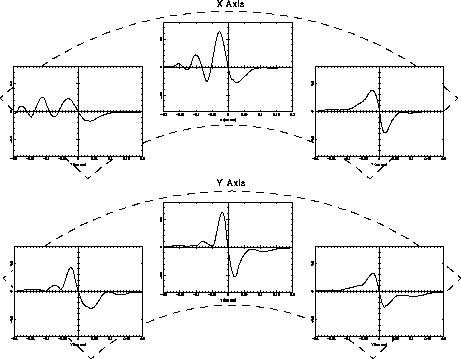
Figure 9.10: Field Dependency of FGS1R Across the Pickle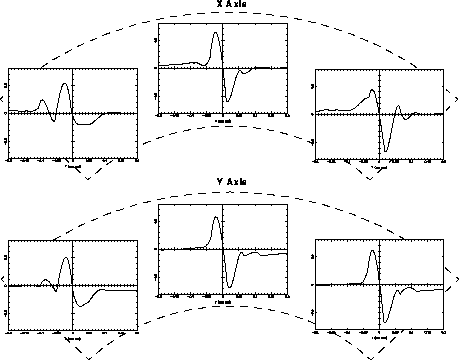
[Top] [Prev] [Next] [Bottom]
stevens@stsci.edu
Copyright © 1997, Association of Universities for Research in Astronomy. All rights
reserved.
Last updated: 11/13/97 16:49:53

Note that the FGS (x,y) detector coordinate system differs from the POS TARG coordinate system in the Phase II proposal instructions. The FGS coordinates originate from the telescope's optical axis (V1 bore sight) while the POS TARG system originates from the center of the detector's field of view. The POS TARG system is used to convienently definte offsets.





 The face of the Koesters prism is 50 mm wide. In the presence of spherical aberration from the telescope's primary mirror, a decentering of the wavefront by only
0.25mm will decrease the modulation of the S-curve to 75% of its perfectly
aligned value. It has been determined that the decenters in FGS 3 range across the
pickle from +0.8 to -0.68 (mm) in x and +0.31 to -0.28 (mm) in y. If the telescope
were not spherically aberrated, mis-alignments up to 5 times this size would not
be noticeable.
The face of the Koesters prism is 50 mm wide. In the presence of spherical aberration from the telescope's primary mirror, a decentering of the wavefront by only
0.25mm will decrease the modulation of the S-curve to 75% of its perfectly
aligned value. It has been determined that the decenters in FGS 3 range across the
pickle from +0.8 to -0.68 (mm) in x and +0.31 to -0.28 (mm) in y. If the telescope
were not spherically aberrated, mis-alignments up to 5 times this size would not
be noticeable.



