[Top] [Prev] [Next] [Bottom]
28.5 Dithering
The pixels of the PC undersample the point spread function (PSF) of the HST by a factor of about two, and the pixels of the WF are a factor of two coarser yet. Thus WFPC2 does not recover a substantial fraction of the spatial information that exists at the focal plane of the instrument. However, this information is not completely lost. Some of it can be recovered by dithering or sub-stepping the position of the chips by non-integral pixel amounts.
The recovery of high frequency spatial information is fundamentally limited by the pixel response function (PRF). The PRF of an ideal CCD with square pixels is simply a square boxcar function the size of the pixel. In practice, the PRF is a function not only of the physical size of the pixels, but also the degree to which photons and electrons are scattered into adjacent pixels, as well as smearing introduced by telescopic position wandering. The image recorded by the CCD is the "true" image (that which would be captured by an ideal detector at the focal plane) convolved with this PRF. Thus, at best, the image will be no sharper than that allowed by an ideal square pixel. In the case of WFPC2, in which at least 20% of the light falling on a given pixel is detected in adjacent pixels, the image is even less sharp.
The PRF of an ideal square pixel, that is a boxcar function, severely suppresses power on scales comparable to the size of the pixel. According to the Shannon-Nyquist theorem of information theory the sampling interval required to capture nearly all of the information passed by square pixels is 1/2 the size l of a pixel. This corresponds to dithering the CCD from its starting position of (0,0) to three other positions, (0,1/2 l), (1/2 l, 0) and (1/2 l, 1/2 l); however, in practice, much of the information can be regained by a single dither to (1/2 l , 1/2 l).
The process of retrieving high-spatial resolution information from dithered images can be thought of as having two stages. The first, reconstruction, removes the effect of sampling and restores the image to that produced by the convolution of the PSF and PRF of the telescope and detector. The more demanding stage, deconvolution (sometimes called restoration), attempts to remove much of the blurring produced by the optics and detector. In effect, deconvolution boosts the relative strength of the high-frequency components of the Fourier spectrum to undo the suppression produced by the PSF and PRF.
If your observations were taken with either of the two dither patterns discussed above, and if the positioning of the telescope was accurate to about a tenth of a pixel (this is usually but not always the case), then you can reconstruct the image merely by interlacing the pixels of the offset images. In the case of a two-fold dither-that is images offset by a vector (n + 1/2, n + 1/2) pixels, where n is an integer-the interlaced images can be put on a square grid rotated 45° from the original orientation of the CCD (see Figure 28.2, top). In the case of a four-fold dither, the images are interlaced on a grid twice as fine as the original CCD and coaligned with it (see Figure 28.2, bottom).
Figure 28.2: Interlacing Pixels of Offset Images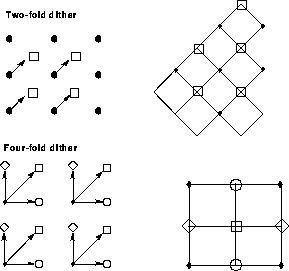
As part of the Hubble Deep Field project, a new method was developed to linearly reconstruct multiple offset images. This method, variable pixel linear reconstruction (also known as drizzle), can be thought of as shifting and adding with a variable pixel size. For poorly sampled data, the shifted pixels retain the initial pixel size-the final image combines the shifts correctly, but the gain in resolution is minimal. For a well-sampled field, such as that of the Hubble Deep Field, the size of the shifted pixels can be made quite small, and the image combination becomes equivalent to interlacing. Drizzling also corrects for the effects of the geometric distortion of WFPC2; correction of geometric distortion is important if shifts between dithered images are of order ten pixels or more.
The drizzle task will soon be incorporated directly into STSDAS as part of a new package called dither. This package will contain not only drizzle, but also new tasks to help the user align images. We have also developed a suite of scripts that can be used to remove cosmic rays and chip defects from singly-dithered images (i.e., only one exposure is taken at each dithered pointing). A preliminary version of this suite has been presented at the 1997 HST Calibration Workshop (Mutchler and Fruchter, 1997). The drizzle software and documentation can be obtained over the web at:
http://www.stsci.edu/~fruchter/dither
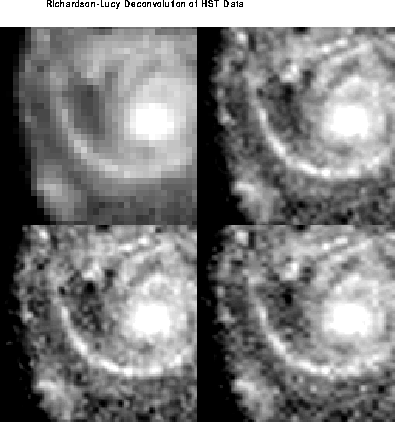
Although reconstruction largely removes the effects of sampling on the image, it does not restore the information lost to the smearing of the PSF and PRF. Deconvolution of the images, however, does hold out the possibility of recapturing much of this information. Figure 28.3, supplied by Richard Hook of the ST-ECF, shows the result of applying the Richardson-Lucy deconvolution scheme to HST data, used extensively in the analysis of WF/PC-1 data. The upper-left image shows one of four input images. The upper-right image shows a deconvolution of all of the data, and the lower two images show deconvolutions of independent subsets of the data. A dramatic gain in resolution is evident.
Figure 28.3: Richardson-Lucy Deconvolution of HST Data
A version of the Richardson-Lucy (RL) deconvolution scheme capable of handling dithered WFPC2 data is already available to STSDAS users. It is the task acoadd in the package stsdas.contrib. In order to use acoadd, users will need to supply the program both with a PSF (which in practice should be the convolution of the PRF with the optical PSF) and with the offsets in position between the various images. Obtaining a position offset between two images is best done by cross-correlating the two images using the task stsdas.analysis.crosscorr. The peak in the cross-correlated image corresponds to the offset between the two images. The peak can be accurately determined using, for instance, imexamine. Even relatively short exposures (a few hundred seconds) on a high-latitude field (such as that chosen for the Hubble Deep Field) allow one to obtain offsets accurate to a small fraction of a pixel. Users will obtain the best results from cross-correlation if the images first have cosmic rays removed (cosmic rays are uncorrelated, and therefore do not bias the result, but can substantially increase the noise in the cross correlation). Users should also taper the images, using the taperedge task in the STSDAS fourier package, to avoid edge effects. In low signal-to-noise cases where the offset is only a few pixels, users may also find it helpful to remove warm pixels to avoid a bias toward zero offset. Once the offsets are determined, the untapered images should be used in acoadd. The process of measuring the shifts between two images will be made considerably easier with the release of dither.
In principle, image deconvolution requires an accurate knowledge of both the instrument PSF and PRF. At present, our best models of the WFPC2 PSF come from the publicly available TinyTim software (Krist, 1995). The quality of the TinyTim model can be improved substantially by taking into account the exact position of the source within the pixel. Remy et al. (1997) discuss how this can be accomplished by generating multiple TinyTim images at various focus and jitter values, oversampled with respect to the camera pixels. At present, this is very labor-intensive, and the results cannot be easily integrated into the existing deconvolution software. Another limitation of the existing software is that it cannot incorporate the significant variation of the PSF across the field of view. As a result, the Richardson-Lucy approach can only be applied to limited regions of a chip at a time. Nonetheless, tests done on WFPC2 images suggest that RL deconvolution can give the WFPC2 user a substantial gain in resolution even in the presence of typical PSF and PRF errors. Users interested in more information on dithering, reconstruction, and deconvolution should consult the February and September 1995 issues of the ST-ECF Newsletter, where these issues are discussed in detail.
[Top] [Prev] [Next] [Bottom]
stevens@stsci.edu
Copyright © 1997, Association of Universities for Research in Astronomy. All rights
reserved.
Last updated: 11/13/97 17:59:14

