|
Starlink and other satellite operators have announced their plans to launch tens of thousands of satellites in addition to the couple of thousands of satellites already in orbit in 2019.
This caused concern in the astronomical community (amateur and professional): will there be more satellites visible in the sky than stars? will astronomy still be possible?
This page tries to give some answer, in a quantitative way, based on what is known about these satellites and what can be simulated. For more detailed information, including technical reports and publications, go to the Reports and Papers section.
|
| Satellites above the VLT. Orange ones are illuminated, grey are in the shadow.
|
Mega-Constellations
Wikipedia: "A satellite constellation is a group of artificial
satellites working together as a system." A mega-constellation is a
group of large constellation, with hundreds or thousands of individual
satellites. The Starlink, OneWeb and others
(see below for a list) aim at providing global
telecommunication coverage, with a very low latency. The low latency
implies a very low altitude, which in turns implies a very large
number of satellites (see the visibility section
below for details.

|
| A constellation of satellites. Each dot is a
satellite, the lines mark the orbital planes.
|
In a typical constellation, the satellite are distributed on a
series of regularly spaced orbital planes. Within each plane, the
satellites are positioned at regular intervals on their orbit (see Walker
1984, JBIS 37, 559).
The planned constellations are evolving quickly, and the number of satellites in orbit is evolving on a weekly basis. The following table lists the known constellations, as of early 2020. We could expect of the order of 75,000 low-orbit satellites in about 10 years from now.
| Constellation | Number of sat | Altitude | Fraction above horizon | Number above horizon | Notes |
|---|
| | | [km] | | | |
|---|
| SpaceX Starlink |
|---|
| SpaceX Starlink v1 2019 | 1927 | | | 472 | (superceded) |
|---|
| SL1 A1 | 2493 | 336 | 2.5% | 62.4 | |
| SL1 A2 | 2478 | 341 | 2.5% | 62.9 | |
| SL1 A3 | 2547 | 346 | 2.6% | 65.6 | |
| SL1 B | 1584 | 550 | 4.0% | 62.9 | |
| SL1 C1 | 1600 | 1110 | 7.4% | 118.6 | |
| SL1 C2 | 400 | 1130 | 7.5% | 30.1 | |
| SL1 C3 | 375 | 1275 | 8.3% | 31.3 | |
| SL1 C4 | 450 | 1325 | 8.6% | 38.7 | |
| SpaceX Starlink rev.2020 | 11927 | | | 366 | |
|---|
| SL1 A1 | 2493 | 336 | 2.5% | 62.4 | |
| SL1 A2 | 2478 | 341 | 2.5% | 62.9 | |
| SL1 A3 | 2547 | 346 | 2.6% | 65.6 | |
| SL1 B1 | 1600 | 540 | 3.9% | 62.5 | |
| SL1 B2 | 400 | 545 | 3.9% | 15.8 | |
| SL1 B0 | 1584 | 550 | 4.0% | 62.9 | |
| SL1 B3 | 375 | 560 | 4.0% | 15.1 | |
| SL1 B4 | 450 | 570 | 4.1% | 18.5 | |
| SpaceX Starlink Gen.2 (2020-05) | 30000 | | | 813 | |
|---|
| SL2 A1 | 7178 | 328 | 2.4% | 175.6 | |
| SL2 A2 | 7178 | 334 | 2.5% | 178.7 | |
| SL2 A3 | 7178 | 345 | 2.6% | 184.3 | |
| SL2 A4 | 2000 | 360 | 2.7% | 53.5 | |
| SL2 A5 | 1998 | 373 | 2.8% | 55.2 | |
| SL2 B | 4000 | 499 | 3.6% | 145.2 | |
| SL2 C1 | 144 | 604 | 4.3% | 6.2 | |
| SL2 C2 | 324 | 614 | 4.4% | 14.2 | |
| OneWeb |
|---|
| OneWeb Original | 648 | 1,200 | 7.9% | 51.3 | (superseded) |
|---|
| OneWeb Ph.2 (2020/05) | 47844 | | | 3790 | |
|---|
| OW2 A | 1764 | 1200 | 7.9% | 139.7 | |
| OW2 B | 23040 | 1200 | 7.9% | 1825.0 | |
| OW2 C | 23040 | 1200 | 7.9% | 1825.0 | |
| OneWeb Ph.2 reduced 2021 | 6372 | | | 505 | |
|---|
| OW2 A | 1764 | 1200 | 7.9% | 139.7 | |
| OW2 B | 2304 | 1200 | 7.9% | 182.5 | |
| OW2 C | 2304 | 1200 | 7.9% | 182.5 | |
| Amazon Kuiper | 3236 | | | 142 | Probably small satellites |
|---|
| Amazon Kuiper 590 | 784 | 590 | 4.2% | 33.2 | |
| Amazon Kuiper 610 | 1 | ,296 | 610 4 | .4% 56 | |
| Amazon Kuiper 630 | 1 | ,156 | 630 4 | .5% 52 | |
| Others |
|---|
| Guo Wang (China) GW-A59 -2 | 12,992 |
| Samsung (Korea) | 4,700 | 2,000 | 11.9% | 561.2 | Microsat
| | Sat Revolution (Poland) | 1,024 | 350 | 2.6% | 26.6 | CubeSat
| | Lynk (USA) | 1,000 | | | | CubeSat
| | GalaxySpace Yinhe (China) | 1,000 | | | |
| | Mangata Network (USA) | 791 | | | |
| | Hongyan CASC (China) | 320 | 1,100 | 7.4% | 23.5 |
| | China Lucky Star | 156 | 1,000 | 6.8% | 10.6 |
| | Commsat Ladybug (China) | 800 | 600 | 4.3% | 34.4 | cancelled?
| | China Xinwei | 32 | 600 | 4.3% | 1.4 |
| | Astrome Tech (India) | 600 | 1,400 | 9.0% | 54.0 | microsat
| | Boing | 2,956 | 1,030 | 7.0% | 205.6 | Transfered applicatoin to OneWeb
| | LeoSat | 108 | 1,423 | 9.1% | 9.9 | Shutdown in 2019
| | Yaliny | 135 | 600 | 4.3% | 5.8 |
| | Telesat LEO | 117 | 1,000 | 6.8% | 7.9 |
| | Roscosmos Sphera (Russia) | ? | | | |
| | Iridium Next (USA) | 75 | | | |
| | Iridium original (USA) | 66 | 780 | 5.5% | 3.6 | deorbited
| | Total | 75,000 | | | 3,000 | (approx) |
|---|
Simulation Techniques
I use 3 techniques to simulate the satellite constellations and their effects:
- Geometric approximation, as used in our paper HW2020: the
geometry of the constellation is simplified in a uniform
sphere. This distorts the distribution of satellites in latitude,
overestimating their numbers at low latitude, underestimating it at
latitudes close to the actual inclination of the satellites, and
overestimating it again above these latitudes. The advantage however
is that the simulations are then extremely simple, based on basic
geometry.

|
| Density of satellites on their orbital sphere as a
function of latitude, for two Walker constellations with orbital
inclinations of 50 and 80deg, and for the uniform
approximation. From HW20.
|
- Numerical simulation: the position of each individual satellite
is computed fairly realistically (assuming simple keplerian orbits,
no perturbations). For a given position of the observatory, the
apparent position and visibility is computed for each
satellite. This method is fool-proof, but computationally
heavy. Also, as the number of satellites in a region of interest
can be low, the simulations must be repeated to reach a sufficient
statistics.
The method used is very similar to that presented by Johnathan
McDowell in his paper (ApJl 892, 2, 2020).

|
| Example of a numerical simulation of
satellites. The apparent position and illumination of each
satellite is computed individually.
|
- Analytical simulations: the satellites are not considered
individually, but as a density distribution over their orbit. This
distribution is represented (exactly) as a mathematical
function. The various quantities (number of satellites, their
velocity, their magnitude...) is computed analytically. This method
is lightning-fast. A paper describing this method is being
prepared.

|
| Example of an analytic simulation of
satellites, showing the density of satellites on the sky.
|
Satellite Visibility
For a satellite to be visible from a given place,
- It must be in sight, above the horizon of that place,
- be illuminated by the Sun,
- and be bright enough to be detected.
Elevation of the satellite
Even if a constellation contains many satellites, as they are spread over the whole Earth, only a small fraction of them will be visible from a given place

|
| The observatory is marked with a big black dot; the Earth, represented by a circle, is oriented so that the observatory is at the top. The small dots are the satellites from a constellation. Only those above the horizon of the observatory (marked in blue) can be seen from that place.
|
Let's generalize the "above the horizon" question.
The elevation is the angle between the satellite and the
horizon. An object with an elevation between 0 and 10 degrees will be
very very close to the horizon, and most likely very difficult to see
(trees, clouds, pollution, even mountains will get in the way). Most
professional telescopes cannot point below 20 deg elevations, and most
observations are performed above 30 deg.
The altitude of the satellites above the Earth also has an influence: higher satellites will remain above the horizon (or above any elevation) longer, so a larger fraction of their constellation will be visible. Typically, 3-10% of a constellation is in sight, and about 10x less above 30 deg elevation -- 0.3 to 1%.

|
| Fraction of a constellation in sight, as a function of the satellite altitude, for various elevations above the horizon.
|
Illumination of the satellite
To be visible, a satellite must not only be in sight, but also be illuminated by the sun. Satellites in the shadow of the earth are completely dark. Other illumination sources, like moonlight, starlight, light from earh --either natural or artificial-- are so weak compared to the sun that they cannot make the satellites bright enough to be detectable, at all.
At sunset, the sun still illuminates everything above the observatory. As it moves down below the horizon, the shadow of the earth engulfs more and more satellites.

|
| As the sun moves down, more and more satellites are caught in the shadow of the earth and become invisible. [ESO/L.Calçada]
|
So, the fraction of satellites in sight that are illuminated by the sun is a function of the sun elevation, but also of the altitude of the satellite. Satellites on higher orbits will remain visible longer after sunset. Some of them are so high that they can remain visible during the whole night (just like the moon, which is a very high satellite).

|
| Fraction of the satellites in sight that are illuminated by the sun, as a function of the elevation of the sun below the horizon, for various satellite altitudes. The sun elevation at midnight is indicated for the equinoxes and solstices at Paranal (this changes with latitude).
|
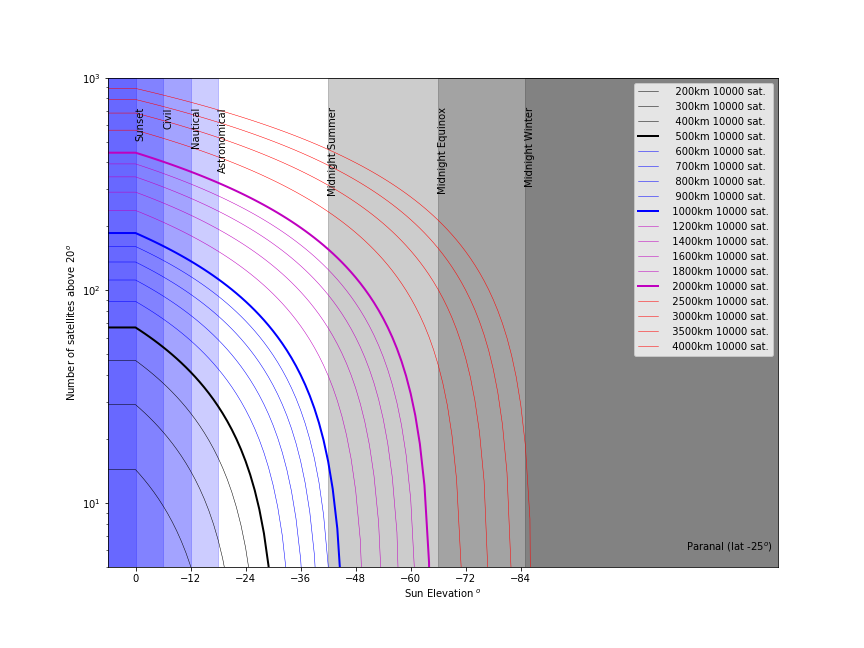
In sight and illuminated satellites
In summary, the number of satellite in sight and illuminated is a function of the elevation of the sun below the horizon, of the size of the constellation and of the altitude of the constellation.
|
|
| Number of satellites in-sight and illuminated as a function of the elevation of the Sun. Each constellation has 10000 satellites. Note the dramatic effect of the constellation altitude
|
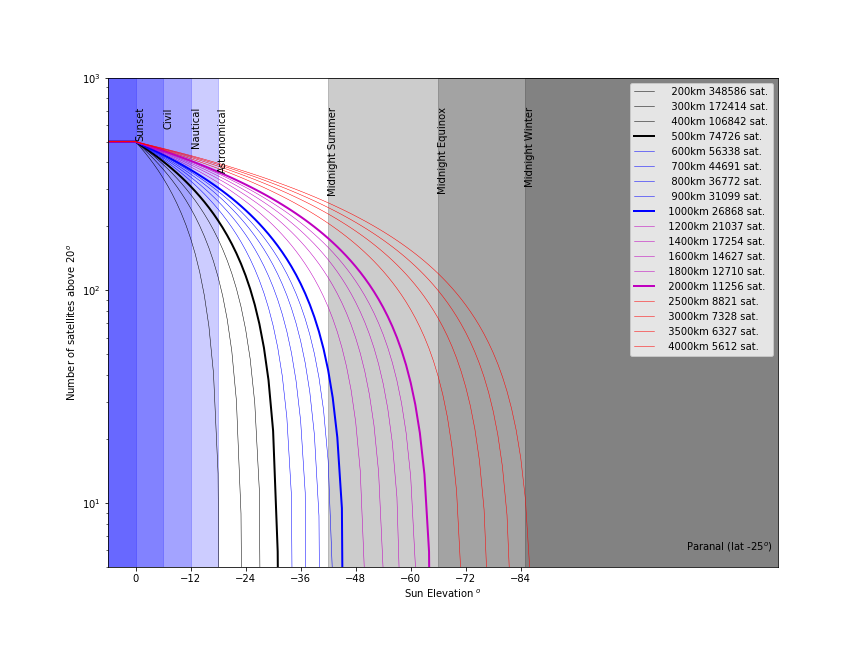
Number of satellites in-sight and illuminated as a function of the elevation of the Sun. The size of the constellations have been scaled so to have 500 satellites above the horizon. Note that this requires 75000 satellites at 500km, but only 11000 satellites at 2000km.
|
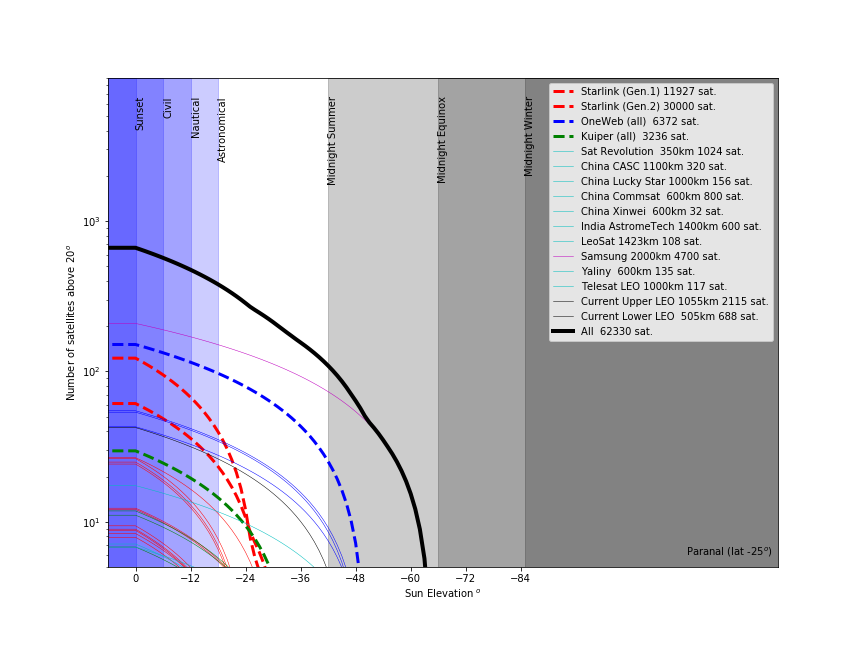
And now with the real, expected constellations. Note that the high altitude OneWeb and Samsung satellites contribute most to the contamination of the dark night; some of them can remain illuminated during the whole night in summer.
|
| Number of satellites above 20deg elevation and illuminated as a function of the elevation of the sun. The twilights and elevation of the sun at solstices and equinoxes are marked, for Paranal. Most constellations known of are represented. The thin red and blue lines represent the individual Starlink and OneWeb subconstellations.
|
Brightness of the satellite
Let's focus here on the visual brightness. For a satellite --or a star-- to be visible, it has to be brighter than a given magnitude (mag is a logarithmic scale; smaller numbers indicate brighter objects; a difference of 5 magnitude indicate that the 2d object is 100x fainter than the 1st one).
The traditional limit for naked eye visibility is mag=7. That is the faintest star that a young person with perfect eyesight will see during a perfectly clear, moonless night from a perfect site. mag=6 is more reasonable for normal people in a good site. For faint moving objects, the limit is even brighter: websites specialized in satellite sighting indicate mag=5 as "very faint" (and the faintest I have ever spotted is ~4).
Computing the magnitude of a satellite is difficult: these are complex bodies, covered with a variety of materials. So, I simplify the problem, and consider that the satellite is a flat panel perpendicular to the line of sight, and scaled to match the measured brightness of Starlink VizorSat. While this is very crude, it is actually not that bad and predicts the magnitude of the satellites within a couple of magnitudes. The reference value is mag=7 for a satellite at 550km above the observatory.

|
| Modeled magnitude of the Starlink satellites as a
function of their distance. The dots are actual measurements
from Otarola et al in the
IAU/UN report.
|
All together
Combining the position of the satellite with that of the Sun, for all the satellites in a constellation, one gets a complete picture of what satellites are visible from a given site. The map below shows the positions of the satellites of a constellation, illustrating what fraction of the constellation is actually visible from two places on Earth.

|
| Positions of the satellites from the Starlink Gen.2 constellation over the Earth at an arbitrary time. The half Earth at night is shaded. The illuminated satellites are yellow, those in the shadow of the Earth are black. Satellites above the horizon of Rubin observatory and London are marked with bold dots. (from Bassa et al, 2022, see ref below).
|
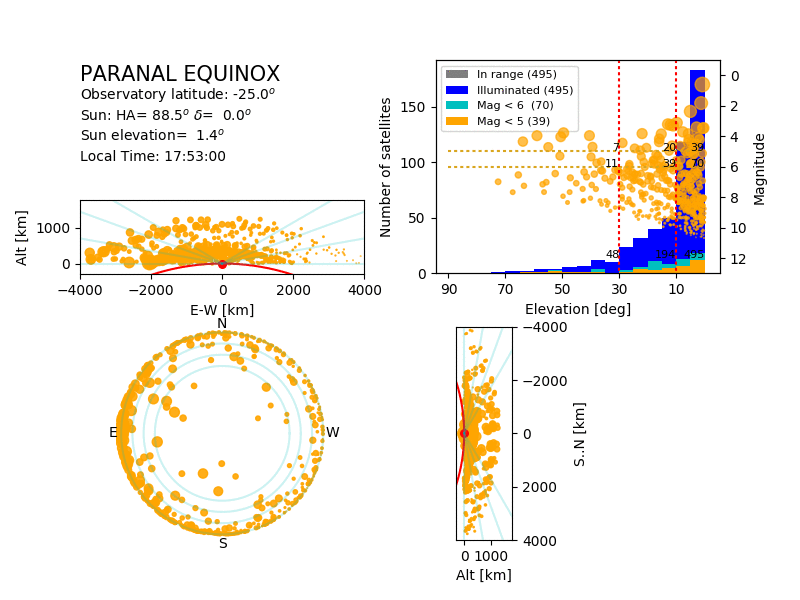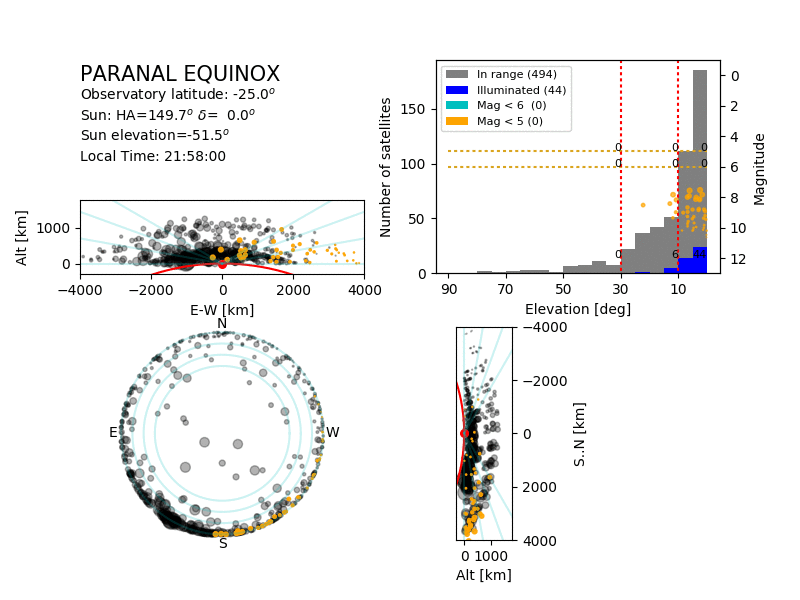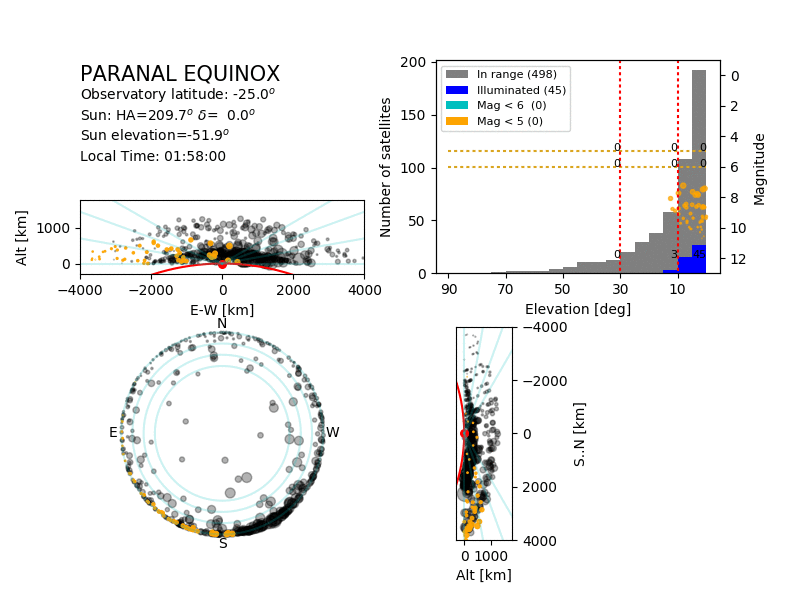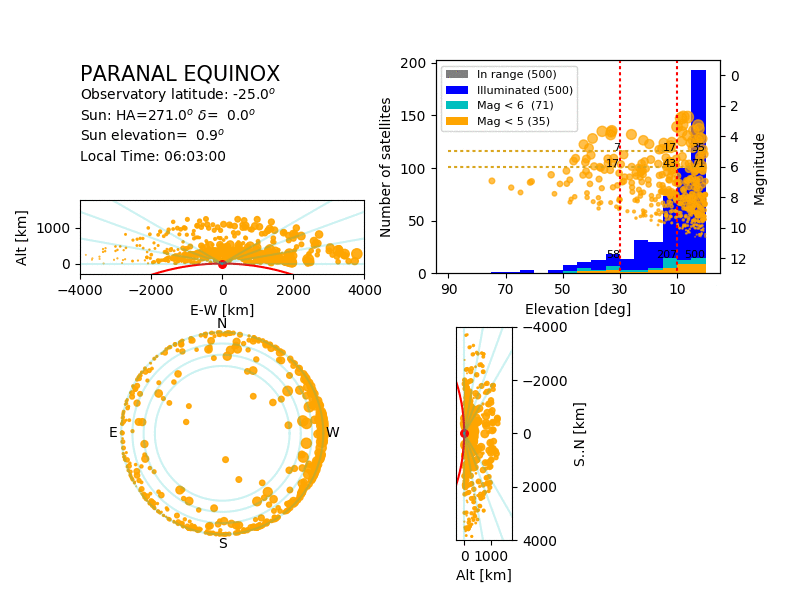
Alternatively, one can simulate what happens during a full night from a given place.
|
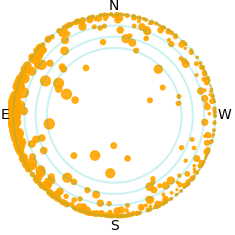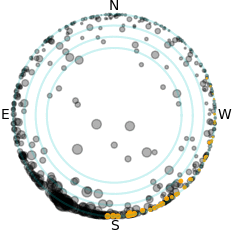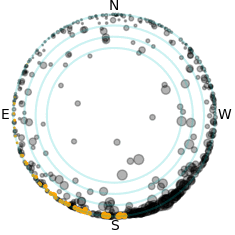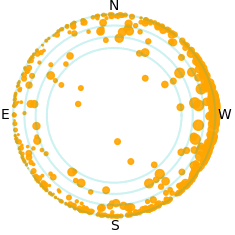
| Simulation of the satellites above Paranal during a
spring night. The bottom left panel shows the position of
the satellites in the sky, the top-left and bottom-right
panels show the same satellites from the side. Yellow
satellites are illuminated, grey are in the shadow of the
Earth. The size of the symbol is related to the magnitude
of the satellite.
The top-right panel shows the magnitude (dot) of the
illuminated satellites as a function of their elevation,
together with the histograms of the satellites (all,
illuminated, and visible to the naked eye) as a function
of their altitude.
The animation covers a full night.
|
Many more plots for other configurations are available on this separate page.
Simulation Results
In what follows, I use the Starlink (generation 1 and 2, 11,927 and
30,000 satellites) and OneWeb (revised/reduced, with 6372 satellites)
constellations, totaling 48,000 satellites on 19 subconstellations
covering low and high orbits. This is a representative set, so the
conclusions are valid for what to expect in ~10 years.
Number of satellites during the night
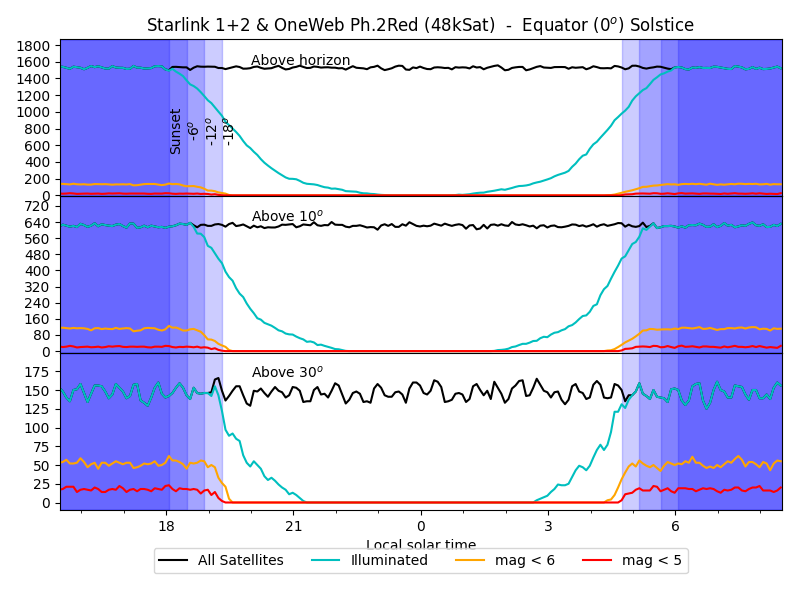
Let's count how many satellites are in sight and illuminated during the night, using a spring night in Paranal as an example.
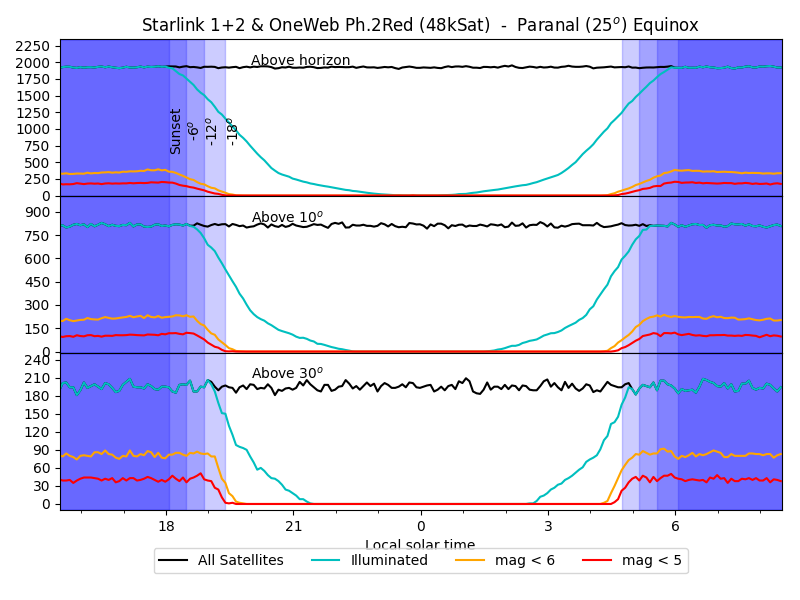 |
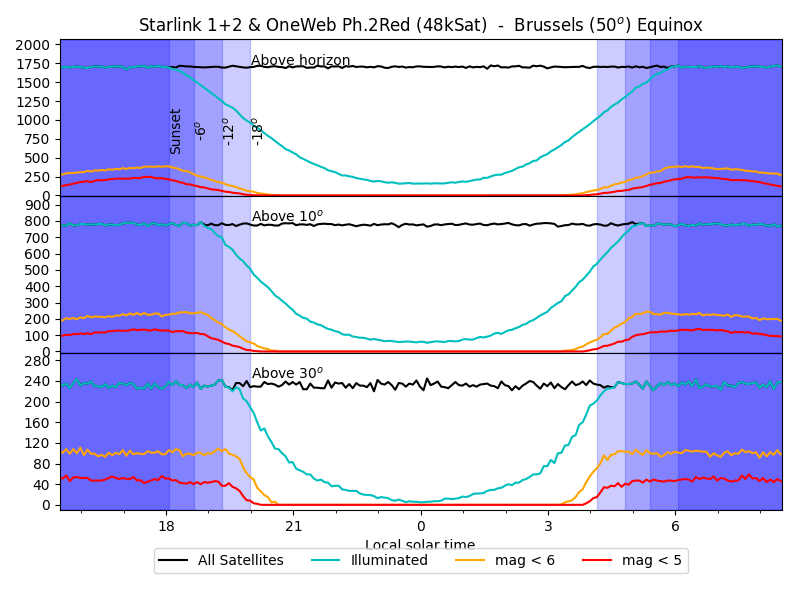
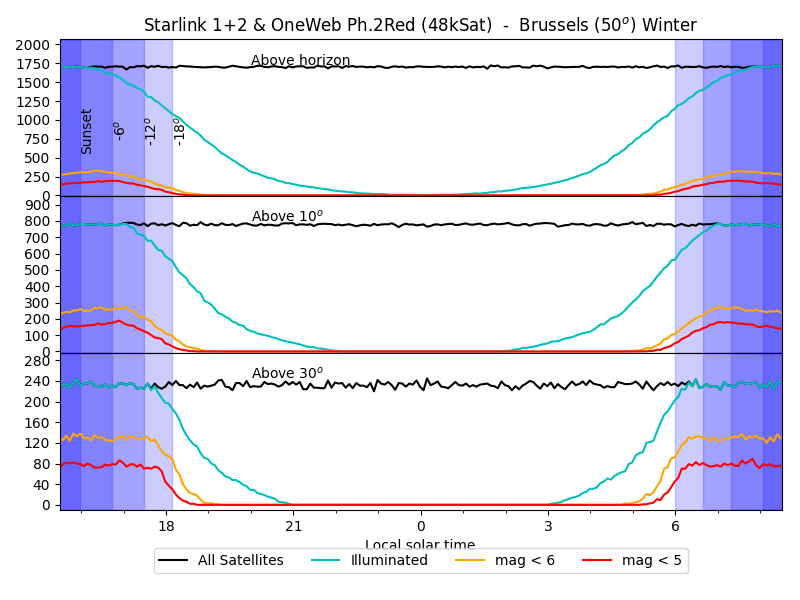
Number of satellites above Paranal (25deg latitude) at equinox, as a function of local time.
- Top panel counts all the satellites above the horizon,
- Second, the satellites above 10deg elevation, for visual observations,
- Third, those above 30deg elevation, for most astronomical observations.
The black line shows all satellites (illuminated or not),
cyan: those that are illuminated, yellow and red: those
visible with naked eye.
The twilights are shaded in blue.
|
About 2000 satellites are above the horizon at any time (top panel,
black line); that number drops to 800 above 10 degrees: most
satellites are clustered on the horizon; about 200 are above 30deg
elevations where telescopes observe most of the time.
The number of illuminated satellites (cyan line) drops after sunset: about half are left at the end of the twilight (shaded blue).
Finally, the number of satellites visible with the naked eye
(yellow for perfect site and perfect eyesight, red for otherwise) is
below a handful (about 10) at the end of the twilight. So, no, there
will not be more bright satellites than stars in the sky.
As discussed in the section on satellite
visibility, that number is a function of the elevation of the sun,
which in turn is a function of the location (and its latitude) and of
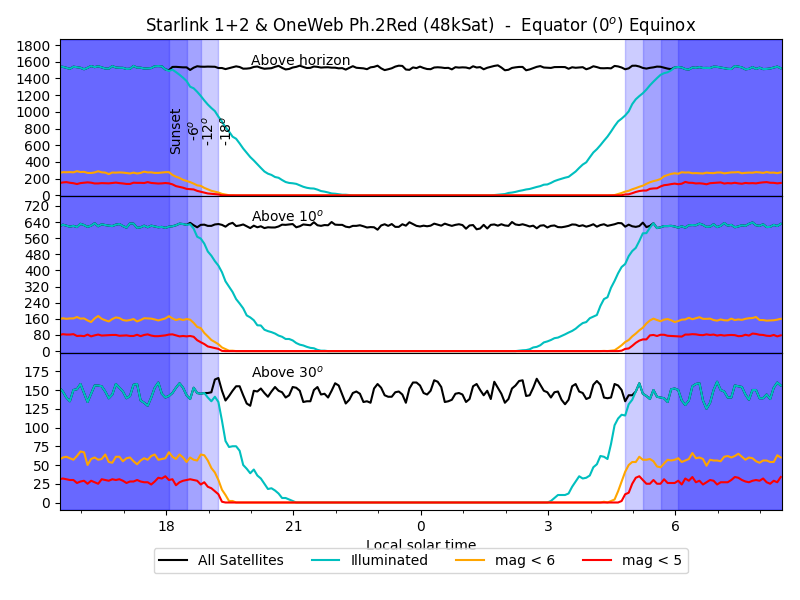
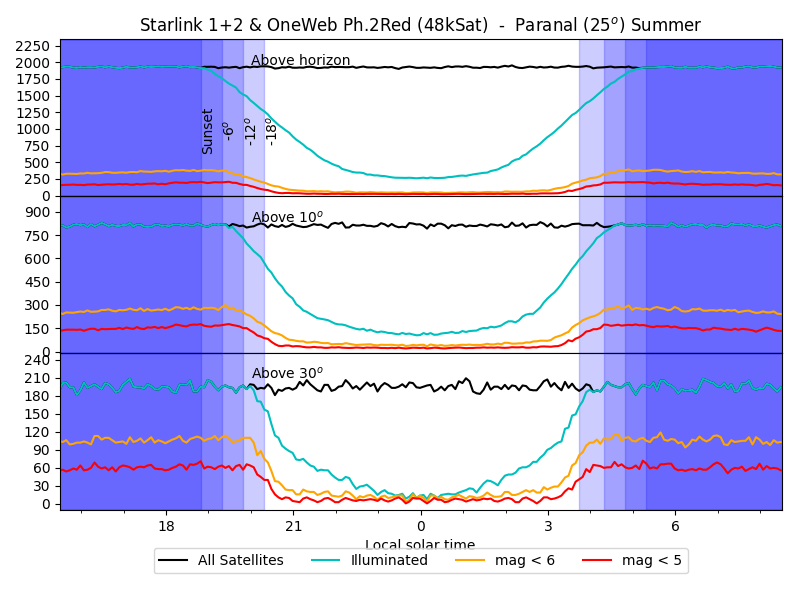
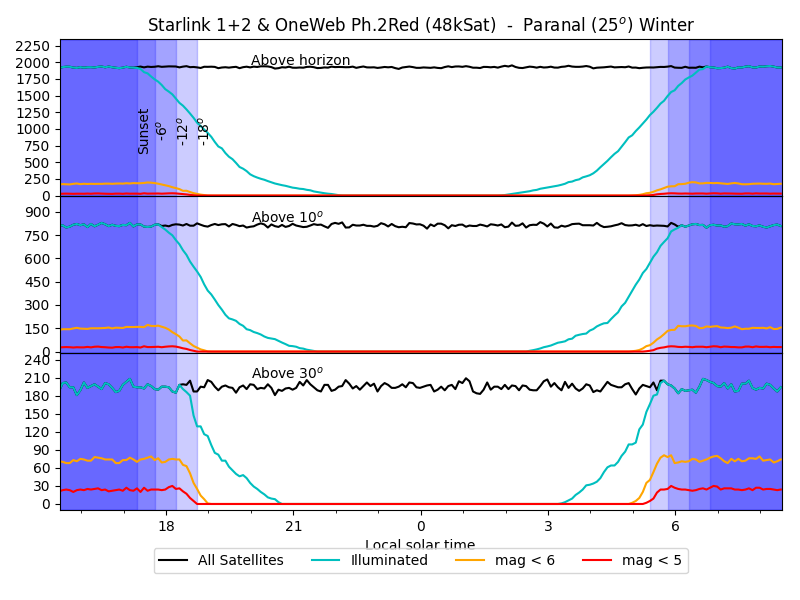
the season. The clickable plots below show the situation at 0, 25 and
50deg of latitude, at summer solstice, equinox, and winter solstice.
Note that, at the equator, both solstices are equivalent. And at
high latitude (like Brussels), the night is never completely dark in
summer.
| Summer | Equinox | Winter |
|---|
| 0deg, equator
| 
| 
|
|---|
| 25, Paranal
| 
| 
| 
|
|---|
| 50, Brussels
| 
| 
| 
|
|---|
The noise and wiggles are an effect of the numerical simulation: it counts actual satellites, so their number varies as satellites appear and disappear.
Many more similar plots, comparing other latitudes and constellations, are available on this separate page.
Effect on observations
To simulate the effects of the satellites on the observations with
a given telescope and instrument, a possibility would consist in
running the numerical simulation over a period of time, and count the
number of satellites which cross the field of view. This is possible,
but numerically extremely intensive: the position of each of the
60,000+ satellites must be computed every second or so over a period
of time. For instruments with small fields of view, this will require
extremely long periods in order to get a few counts.
A much more efficient way is to evaluate the density of satellites
trails in the region of interest in the sky. This can be done
analytically, which has the advantage of a much greater precision and
to be extremely fast. A paper describing this
method is in preparation.
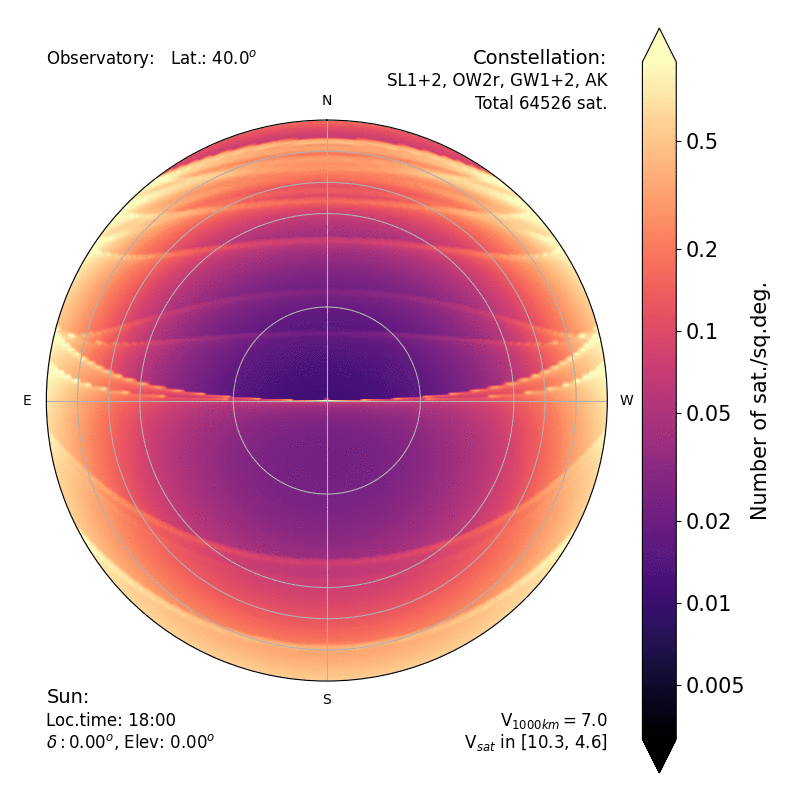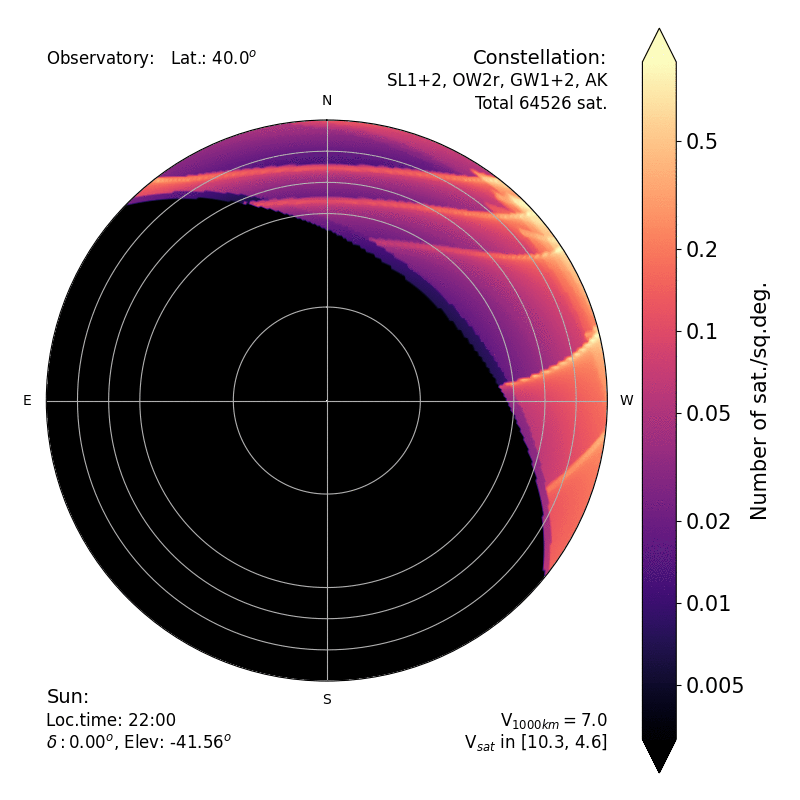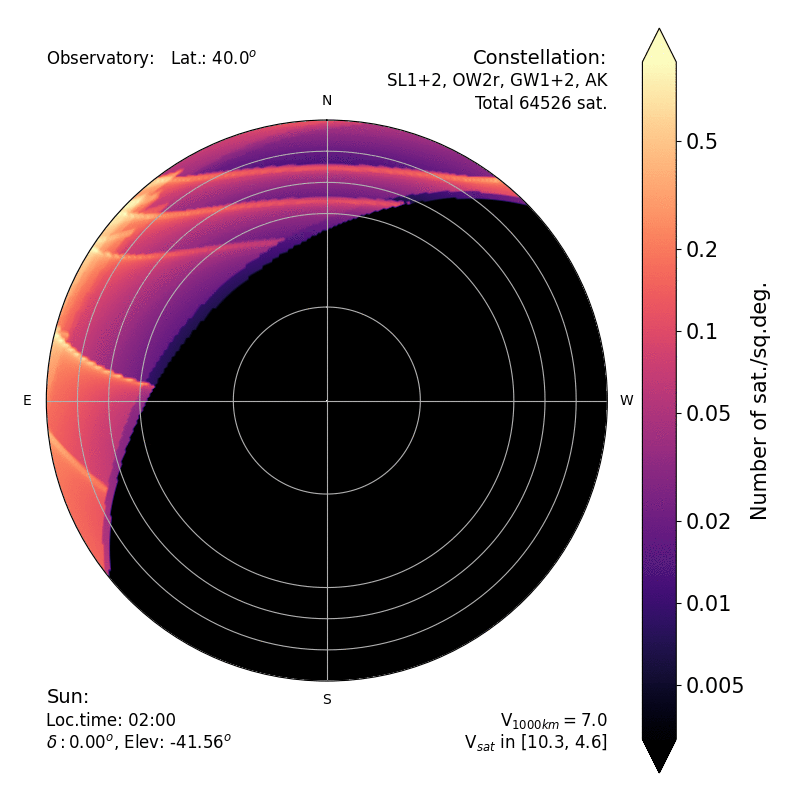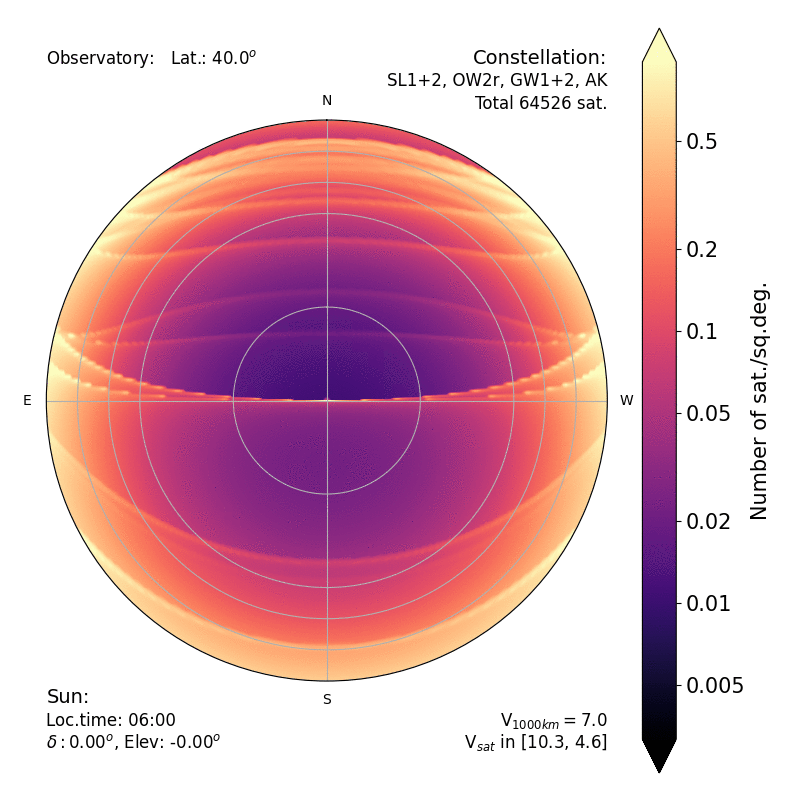 |
| Density of satellites (in sat per square deg) over
the sky, computed analytically. The black croissant to the
East represent the region of the sky where all satellites
are already in the shadow of the Earth. The various
crescent boundaries correspond to the edge of the shadow
on lower constellations. The brighter areas extending from
East to West are the edges of the constellations whose
inclinations are close to the latitude of the site.
|
Another advantage of this analytical method is that it reveals sharp structures caused by the geometry of the various subconstellations.
To compute the effect on observations, the instantaneous density of satellite is not sufficient. One must take into account their motion: a fast moving satellite will affect a larger region than a slow one. This is represented by the trail density, obtained by multiplying the local density of satellites in a constellation by the average velocity of these satellites. Armed with the satellite and trail densities, on can compute the number of trails that will affect an observation.
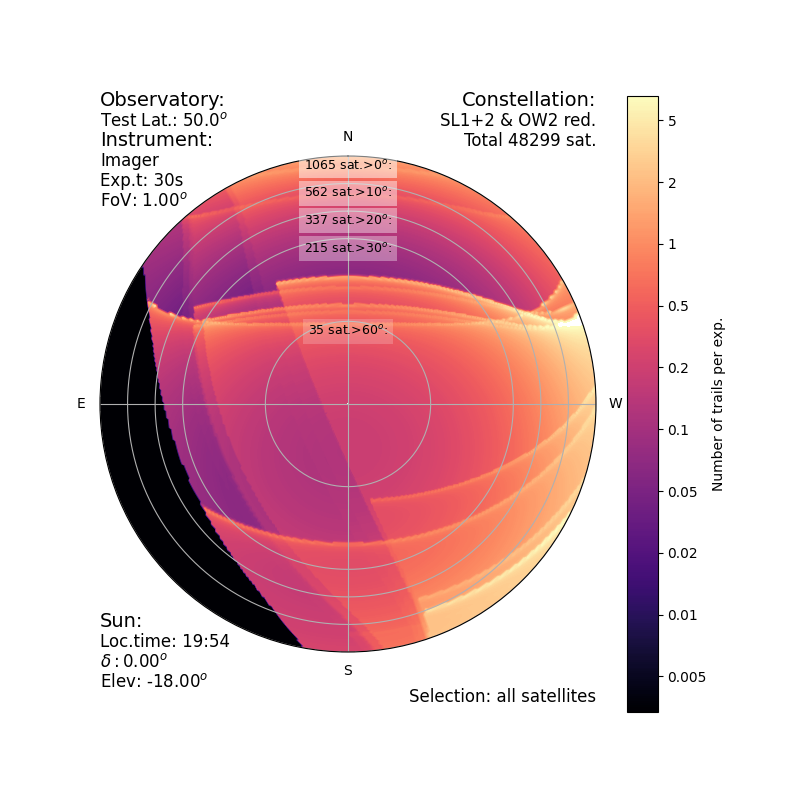 |
| Number of trail per exposure, for an camera with a 1sq.deg. field of view, as a function of the position of the observation in the sky, at the end of twilight.
|
This figure shows that a 30s exposure will (at twilight at zenith) on average has ~1 satellite crossing each image. Of course, that is not the full story: this plots accounts for all satellites, of any magnitude. The effect of the magnitude will be very different depending on the observation technique.
As an example, for a camera mounted on a large telescope, a bright satellite (say, brighter than magnitude 7) could saturate the detector and ruin the complete exposure, while a fainter satellite will only leave a trail a few arcseconds wide. The characteristics of each instrument has to be taken into account.
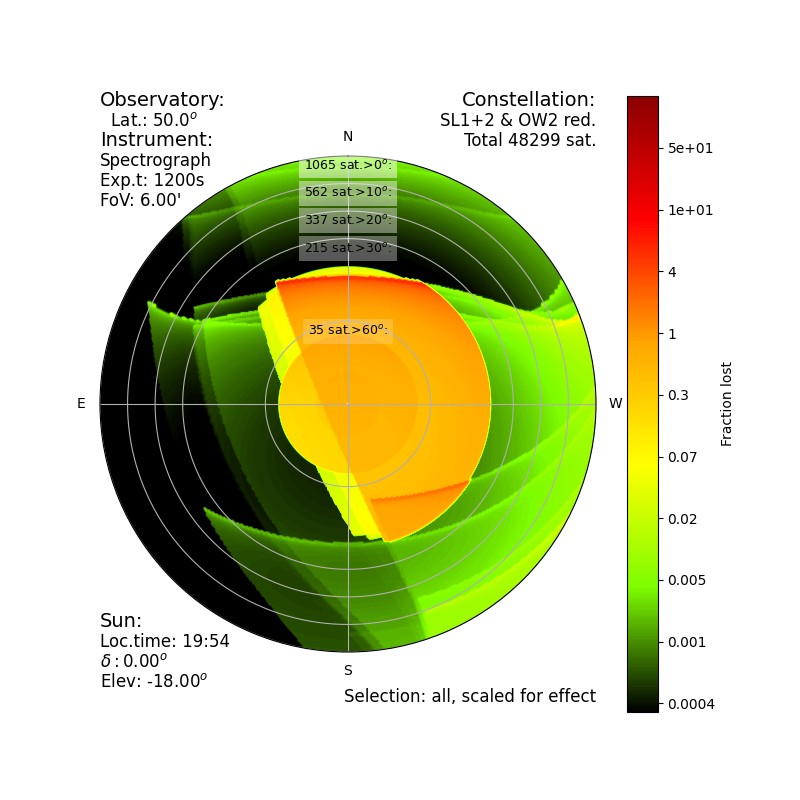 |
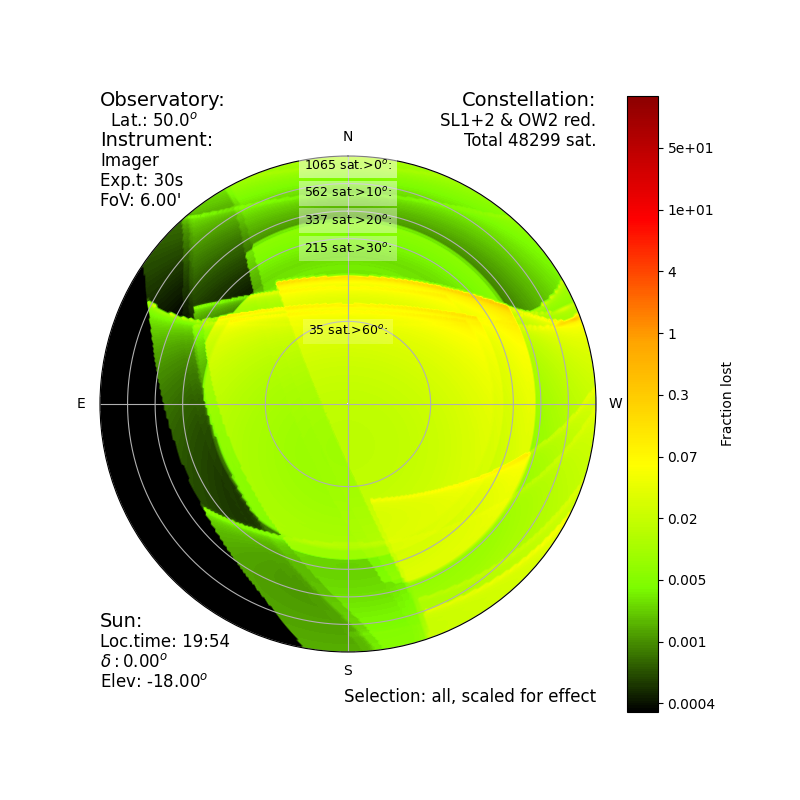 |
|
Fraction of lost exposures for an hypothetical spectrograph
|
Fraction of lost exposures for an hypothetical imager
|
The software used to generate these plots is available as a simple web tool in the simulators page. They are also available on GitHub:ohainaut/SatConAnalytic.
Reports and Papers
Reports:
- Report to ESO Council, 2020-Nov. PDF: a summary of the effect on visible and radio astronomy, and of the mitigation at the technical and policy levels.
- UN/IAU Dark and Quiet Skies for Science and Society, 2020-Oct. PDF. Comprehensive report including light pollution, radio pollution, and satellite constellations.
- SATCON1, AAS report to NSF, 2020-Aug. Report PDF, Technical appendices PDF
- SATCON2, AAS report to NSF, 2021-Oct. Report PDF
- UN/IAU Dark and Quiet Skies for Science and Society 2, 2021-Oct. PDF
Technical paper:
- Hainaut & Williams 2020 AA 636, A121: PDF, geometric simulations of the effects of constellations on observations.
- Bassa, Hainaut, Galadi 2022 AA 657, A75: PDF
, analytical simulations of the effects on observations. Supersedes H&W2020
|