3.1 Multiplex gain

In order to determine the number of galaxies that can be observed simultaneously with IFS and MOS, it is necessary to take into account the density of galaxies, the field of view of each design, as well as those factors which restrict the multiplex gain in the MOS (eg, crowding and edge factors).

Galaxy Counts

The basic information we have used to infer the number of galaxies in the field of view are the papers by:

• Yan et al. (ApJ, 503, L19, 1998; HST-parallel for H < 24.5)
• Bershady et al (ApJ, 505, 50, 1998; Keck for K < 23)
• Thompson et al (AJ, 117, 17, 1999; NICMOS-HDF for H_AB < 28.8)
• HDF-S at www.stsci.edu/ftp/science/hdfsouth/catalogs.html

The uncertainties at faint magnitudes are still important. For instance, in the Thompson et al data these are due to:

0. the relatively small field observed with NICMOS which may not be representative,
1. errors in the determination of magnitudes (eg, magnitudes obtained with SExtractor and those inferred from KFOCAS differ by 1 magnitude at H_AB(KFOCAS) = 29: for H_AB < 27 the agreement is good), and
2. statistical errors (especially at a given magnitude bin), due to the relatively reduced number of objects observed. Bershady et al give about 500,000 galaxies/mag/degree at K_AB=25, while HDF-S has about 200,000.

There are also uncertainties in the completeness factors. Here all the data have been corrected by completness according to table 5 column Cs16 by Thompson et al. We have established K_AB = 27.5 mag as the limit where the uncertainties become too large.

In table 1 the mean number counts used here are given.

 

Table 1: Galaxy number counts

			MOS	MOS	IFS-LR	IFS-LR	IFS-HR	IFS-HR
KAB	N/mg/deg	N/deg	N/mg/fov	N/fov	N/mg/fov	N/fov	N/mg/fov	N/fov
19.5	9000.	8999.	29.	29.	1.	1.	0.	0.
20.0	13500.	14624.	43.	47.	2.	2.	0.	0.
20.5	18000.	22499.	58.	72.	3.	3.	0.	0.
21.0	25000.	33249.	80.	107.	4.	5.	0.	0.
21.5	32000.	47499.	103.	153.	5.	7.	0.	0.
22.0	45000.	66749.	144.	214.	6.	9.	0.	0.
22.5	58000.	92499.	186.	297.	8.	13.	0.	0.
23.0	79854.	126963.	256.	408.	11.	18.	0.	0.
23.5	102155.	172463.	328.	554.	15.	24.	0.	0.
24.0	134200.	231551.	431.	744.	19.	33.	0.	0.
24.5	166962.	306841.	536.	985.	24.	44.	0.	0.
25.0	216564.	402722.	695.	1293.	31.	57.	0.	0.
25.5	268413.	523966.	862.	1683.	38.	74.	0.	0.
26.0	346572.	677712.	1113.	2176.	49.	96	0.	1.
26.5	435380.	873200.	1398.	2804.	62.	124.	0.	1.
27.0	540670.	1117212.	1736.	3587.	77.	159.	0.	1.
27.5	695894.	1426353.	2235.	4580.	99.	203.	1.	1.
28.0*	(1011256)	(1853140)	(3247)	(5951)	(144)	(263)	(1)	(1)
28.5*	(1914016)	(2584458)	(6146)	(8299)	(272)	(367)	(1)	(2)

(*)Values within brackets are not reliable. Corrected for completeness according to table 5 column Cs16 by Thompson et al.

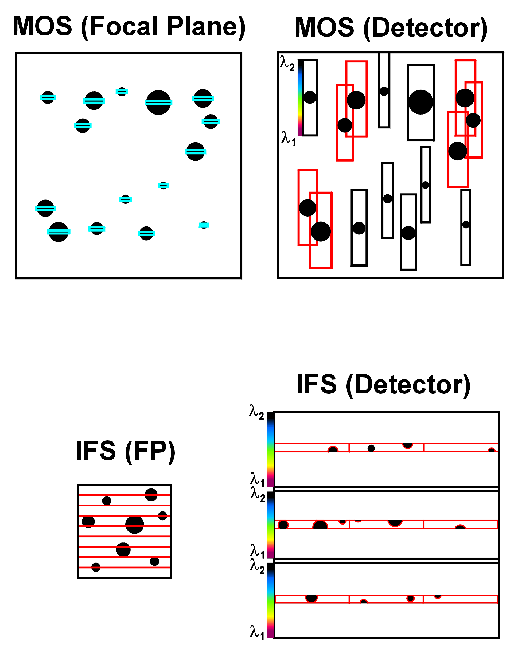
If galaxies are relatively close together, they cannot be observed simultaneously with MOS as their spectra overlap on the detector. This situation is illustrated schematically in figure 1. In the IFS, this problem never occurs since the spectra are uniquely ordered on the detector.

 

Figure 1: Ilustration of how some spectra overlap in the MOS design. This type of problem never occurs in the IFS.

Crowding factors

The fraction of galaxies with such a conflict will depend on:

0. The density of galaxies (number counts),
1. the galaxy size (slit length),
2. the spectrum length.

The observed number counts were discussed in the previous section. For the slit length, a value of 5 times the half-light galaxy diameter (10 x r_1/2) is used. This relatively large slit length is justified in order to obtain local background information. Depending on calibration stability, it may be possible to utilise separate apertures distributed throughout the field, in which case the slits could be shorter. For the spectra, a length of 514 pixels is used. This value is derived using the grating R=300 in the range 0.8-2.0 microns. (It is assumed that for MOS R = 150 is obtained with a slit of 0.2'' wide, i.e. 2 micro-mirrors lines). Note that for higher resolutions, this problem is generally more important since the spectra need to be relatively larger in order to have a reasonable spectral coverage.

The calculations were done by generating galaxies at random positions according to the observed number counts and sizes, and analysing the conflicts on the detector. The code we use maximises the number of galaxies that can be observed simultaneously.

In addition to the crowding factors, a galaxy close to the edge of the FOV in the MOS design will have part of its spectrum outside the detector. This basically depends on:

0. The detector size (4K x 4K), and
1. the spectrum length (and marginally on its width).

For the case under study (Spectrum length 514 pixels, detector 4K x 4K) this represents about 12.5% of the total number of galaxies in the FOV.

As proposed by MacKenty in his report, rectangular arrays or detectors may reduce this problem, but these alternative designs will have implications in terms of pixelation, spectrograph size/weight, etc. Therefore, here we will retain the baseline square arrays for the MOS design.

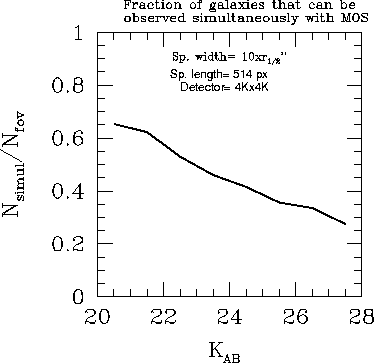
In figure 2, the fraction of galaxies that can be observed simultaneously for the MOS baseline design (at R=150) is presented. This curve includes the edge factors which, in this case, amount to about 12.5%.

 

Figure 2: Fraction of galaxies which can be simultaneously observed with a MOS design for a slit length of 10 x r_1/2, a spectrum length of 514 pixels, and a 4K x 4K detector. This curve includes the edge effects which amount to 12.5%.

Note that these results correspond to mean densities and mean sizes at a given magnitude. For specific programs involving clustered sources, these values can be rather different.

Multiplexing gain: Results

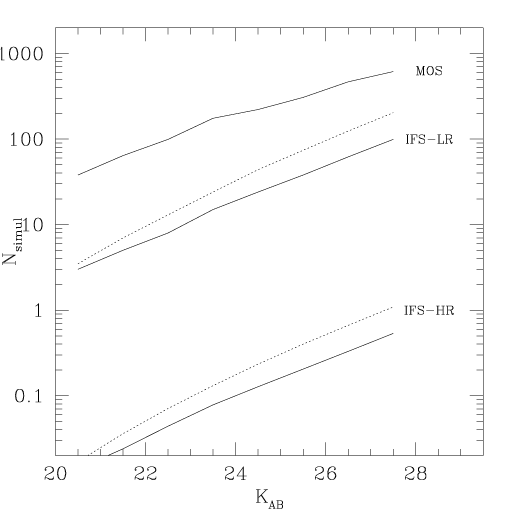
Figure 3 presents the number of objects in the field of view that can be observed simultaneously.

 

Figure 3: Number objects in the field of view that can be observed simultaneously with IFS-HR (bottom), IFS-LR, and, MOS (top) designs versus K_AB (continous line: number/mag/fov; dot line: number/fov, ie, cumulative). The curve corresponding to the MOS design has been corrected with the crowding factors (figure 2)