3.2 Exposure times

The IFS and MOS concepts extract the information from the focal plane in a rather different way and they arrange the spectra on the detector differently. The proposed baseline designs also have different spatial pixels which project onto a different number of detector pixels. The estimation of their relative figure of merit is therefore not straightforward.

Here we will analyse their relative sensitivities taking as reference their baseline designs. We compare the exposure time required by IFS and MOS to observe a single faint galaxy (K_AB > 20 mag) at a given magnitude. This is done for R=150 and $\lambda$ = 2.2 microns, although the effects of considering other resolutions and wavelengths are addressed. For MOS, it is assumed that R = 150 is obtained with two lines of micro-mirrors, giving a slit width of 0.2".

The generic formula which relates the S/N (per object, not per pixel) and the exposure time (t) in a standard imaging instrument at a given resolution is:

$$S/N={T \cdot N \cdot t \over \sqrt{N \cdot t \cdot (T+Z+Dr) + N_{split} \cdot N \cdot RO}}$$

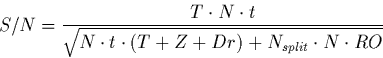
where,

T : is the mean target flux in counts/spatial pixel/spectral resolution element/sec
N : is the number of pixels comprising the image of the source
Z : Zodiacal light flux in counts/spatial pixel/spectral resolution element/sec
Dr: Dark current in counts/pixels/sec
RO: Read noise in count/pixel
N_split : Number of frames in which each exposure is split to avoid excessive cosmic ray contamination or to avoid filling the detector wells. After each frame a readout is performed.

For long exposures this formula can be approximated:

$$S/N={T \cdot N \cdot t \over \sqrt{N \cdot t \cdot (T+Z+Dr) +... ...cdot N \cdot t \over \sqrt{N \cdot t \cdot (T+Z+D)}}, \eqno(1)$$

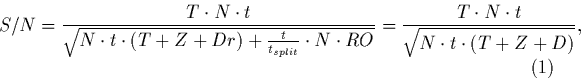
where t_split is the unit exposure time (960 sec, usually - determined by the cosmic ray rate), and

$$D={Dr + {1.\over t_{split}} \cdot RO}$$

This formula can be solved directly.

For IFS and MOS, equation (1) applies in a different way due to the fact that the spatial pixels at the focal plane do not correspond to the pixels on the detector. In particular,

For IFS, and considering that one spatial pixel (about 0.2'' x 0.2'') at the focal plane projects into 2 x 1 pixels at the detector, equation (1) is transformed into:

$$(S/N)_{ifs}={\epsilon_{ifs} \cdot T \cdot N_{ifs} \cdot t_{if... ...ot t_{ifs} \cdot [\epsilon_{ifs} \cdot (T+Z) + 2D]}}, \eqno(2)$$

where, $\epsilon_{ifs}$ is the relative efficiency (throughput) of IFS and N_ifs is the number of spatial pixels (at the focal plane) comprising the image.

For MOS, and taking into account that 0.2'' x 0.2'' on the focal plane (2 x 2 micro-mirrors) project into 4 x 4 pixels on the detector, equation (1) is transformed into:

$$(S/N)_{mos}={\epsilon_{mos} \cdot T \cdot N_{mos} \cdot t_{mo... ...t t_{mos} \cdot [\epsilon_{mos} \cdot (T+Z) + 16D]}}, \eqno(3)$$

where, $\epsilon_{mos}$ is the relative efficiency (throughput) of MOS and N_mos is the number of spatial elements of 0.2" x 0.2" (formed by 2 x 2 micro-mirrors) forming the slit. For very small objects (say, r_1/2 < 0.5", MOS can adjust better its spatial element to the object size in the spatial direction, and some correction will be applied (see below). However, this only occurs at the very faintest magnitudes.

Therefore, at equal S/N (per object), the relation between the exposure times for MOS and IFS is:

$${t_{mos} \over t_{ifs}}=\left({\epsilon _{ifs} \... ...mos} +16 D\over (Z+T) \epsilon _{ifs} + 2 D }\right], \eqno(4)$$

This formula represents the main features to be considered when comparing the sensitivity of the two spectrographs.

The first bracket represents the importance of their relative troughput. In fact, t_mos/t_ifs goes with the square of the relative sensitivity for faint objects. For bright objects (D is negligible) the t_mos/t_ifs is linear with ifs/mos throughput ratio.

The second bracket represents the slit-losses in the MOS. In fact, N_ifs/N_mos is always > or equal to 1. The larger the object the larger the factor N_ifs/N_mos.

The third bracket takes into account the different way in which the spatial pixels at the focal plane are projected onto the detector, weighted by their relative importance with respect to other kinds of noise sources. When the detector noise is negligible (ie, for bright sources and/or low resolution), equation (4) is simplified to :

$${t_{mos} \over t_{ifs}}=\left({\epsilon _{ifs} \over \epsilon _{mos}}\right) \left({N_{ifs} \over N_{mos}}\right)$$

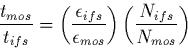
However, for faint objects (or high resolution), the detector noise plays a relevant role and the bracket value approaches 8 as a consequence of the way in which the spatial pixels are projected onto the detector. A tabulation of

$$F=\left[ {(Z+T) \epsilon _{mos} +16 D\over (Z+T) \epsilon _{ifs} + 2 D }\right]$$

is given in the next subsection.

 

Figure 4: (left) from Thompson et al data. (right) Mean values from Thompson et al (full triangles) and Yan et al (open squares). Lines indicate constant mean surface brightness interior a half-light radius.

Quantitative results

For the present analysis we will consider $\epsilon_{mos}$ = $\epsilon_{ifs}$ . However, in a more refined analysis, the packing fraction of the Micro-mirror array (MMA), or equivalent device, and the effects of diffraction and scattered light from the MOS apertures should be taken into account.

For estimating N_ifs/N_mos galaxies are considered to be circular in shape, with radius r_1/2 (half-light radius).. Assuming spatial elements of 0.2'' x 0.2'',

$$\left({N_{ifs} \over N_{mos}}\right)={\pi \cdot \left(r_{1/2}... ...2 \over 2 \cdot (r_{1/2}/0.2)}={\pi \cdot r_{1/2}('')\over 0.4}$$

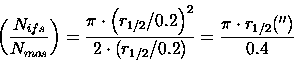
Considering the mean observed values (see figure 4), the following results are obtained for N_ifs/N_mos (at a given K_AB magnitude): 3.4 (20.5), 2.9 (21.5), 2.5 (22.5), 2.1 (23.5), 1.8 (24.5), 1.6 (25.5), 1.2 (26.5), 1. (27.5). Note that for longer wavelengths than that considered here (2.2 microns) the size of the objects is larger as a consequence of the broader PSF, which makes the N_ifs/N_mos larger.

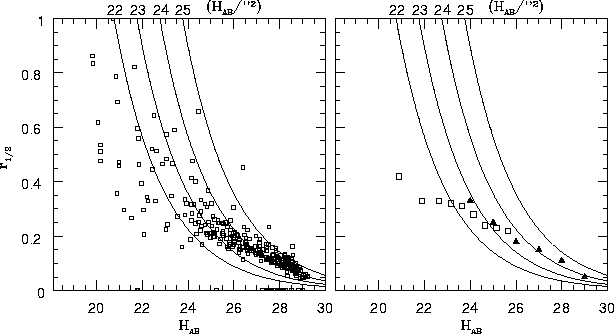
In order to tabulate F, we have determined the flux enclosed in a 0.2'' x 0.2'' spatial pixel, from the mean observed surface brightness of faint galaxies. In Figure 4 (left) the Thompson et al data in the plane H_AB - half light radius are presented, together with lines of constant surface brightness. In Figure 4 (right) the mean data from Yan et al. and Thompson et al. are presented. From this plot the mean surface brightness at a given galaxy magnitude has been determined.

Using these magnitudes and the new exposure time calculator (NSM, Petro et al) the function F has been tabulated for R = 150 assuming $\epsilon_{mos}$ = $\epsilon_{ifs}$ = $\epsilon_{nirspec(nms)}$. The following values (for a given K_AB magnitudes) were obtained: 1.13 (20.5), 1.26 (21.5), 1.51 (22.5), 1.85 (23.5), 2.26 (24.5), 2.51 (25.5), 2.99 (26.5), 2.67 (27.5).

However, as mentioned above, for very small objects (say, r_1/2 < 0.05"), MOS can adapt its spatial element to the object size, reducing the number of detector pixels (and so its noise). In that case a better approach should be

F=[(T*e_mos+(Z*e_mos+16D)/2]/[(Z+T)e_ifs+2D]

Although, we never reach this situation, for K_AB = 27.5 ( r_1/2 ~ 0.12"), we have considered an intermediate approach.

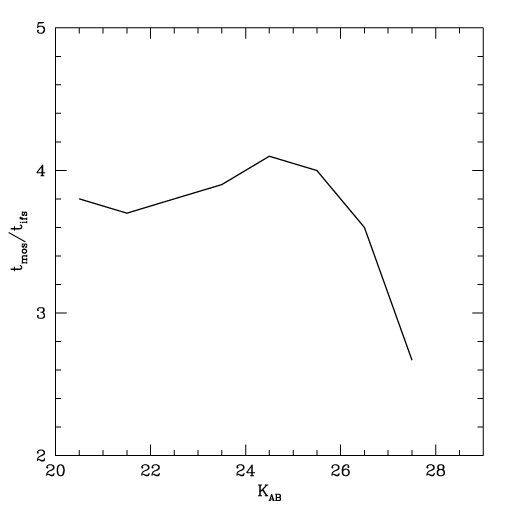
Considering the F tabulation and the N_ifs/N_mos values reported above the t_mos/t_ifs values were derived. In Figure 5 the results are presented. Note that IFS is more sentitive than MOS in the complete range analyzed. The trend at the faintest end is due to the better fit of the MOS aperture size to the object size which reduces both Zodiacal light and, more importantly, detector noise.

 

Figure 5: Relative exposure times between MOS and IFS when observing a single galaxy (of K_AB) at equal S/N per object, and R = 150. The same throughput has been assumed for MOS and IFS. These curves take into account the different way in which the spatial pixels are projected into the detector, and the slit losses of MOS. For the latter, galaxies are assumed to be 2*r_1/2 in diamenter, where r_1/2 is the mean observed half-light radius at a given magnitude (HDF). It is also considered that MOS achieves R = 150 with a 0.2" width slit.