The Venus Transit 2004

... Extended InfoSheet G4

Distances in the solar system: parallax and Kepler's laws

Astronomers observe primarily angles on the sky on what is called the celestial sphere. However, the stars are not all at the same distance from the Earth. Starting from simple measurements of angles, how can we measure the size of the Earth, the distance to the planets and to the stars, and eventually understand the actual motions of objects in space?

The concept of parallax is essential to achieve all this. If two observers see the same object at different angles, that means that the object is not at infinity. The difference in angle depends only on the positions of the observers and on the distance to the observed object. This is the phenomenon of relief, created by our brain using the different images received by our eyes. The greater the distance to the object, the more the observers need to be separated. So we will use this phenomenon to measure the distance to heavenly objects that can not be measured directly. On Earth, the method is used to measure the distance to remote places without going there: it is called triangulation.

Triangulation

Let us start by trying to measure the distance to a remote object on the Earth. In this way we can gradually map the Earth's surface. We use the triangulation method: we see an object in some direction from site n°1(angle V1) and if we move along a known distance called "the baseline", we see the object in a different direction from site n°2 (angle V2). In the triangle "object - site n°1 - site n°2", we know a side and two angles: we can calculate the other sides and determine the distance to the object. In astronomy this effect is called "parallax".

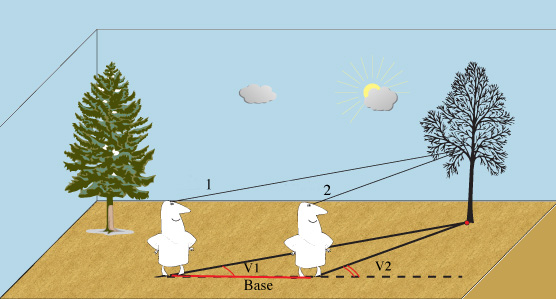
The parallax concept

Parallax in astronomy

To calculate the distance from the Earth to a celestial body, one can proceed in a similar way. From two places on Earth, we can measure the angle of sight of a star and, knowing the length of the baseline, we can calculate the distance. It is easy to see that this method has its limitations if the star is very far away. The greatest terrestrial baseline can not exceed the Earth's diameter of 12,756 kilometres so it is necessary that the difference in the angle of sight of the two observers can be measured with the instruments available.

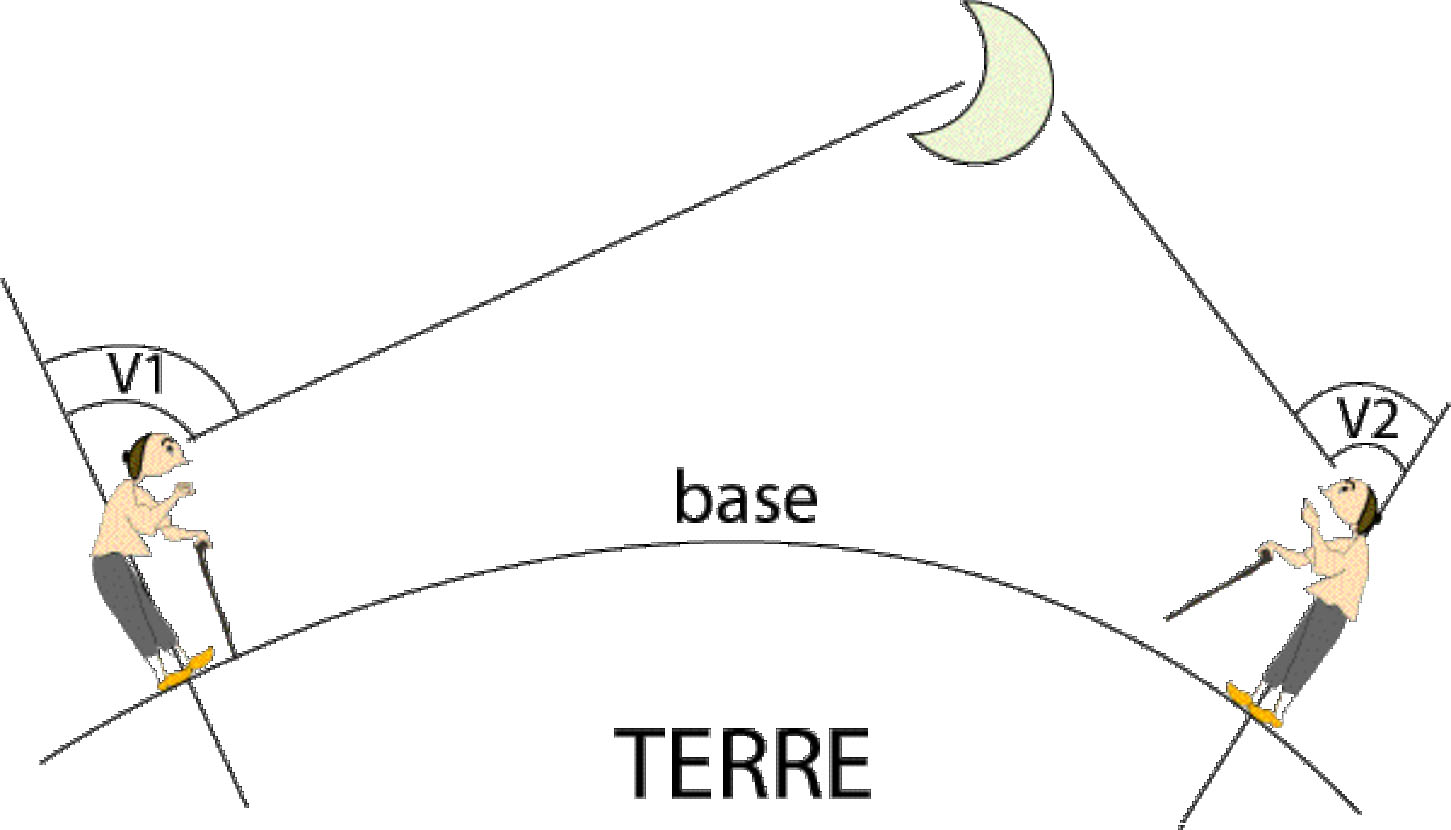
Calculation of a distance using parallax.

Example: Calculation of distance by triangulation

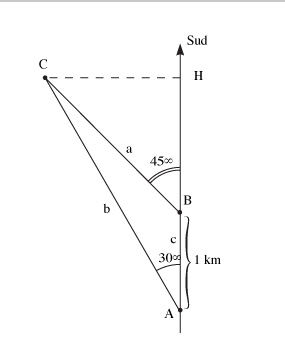
Measure of distance by triangulation

We wish to measure the distance CH between a building C and a road ABH that lies along the north-south direction in which an observer is travelling. The observer can measure only angles or distances along the road. From the position A, the observer measures an angle of azimuth 30° between the building C and the South direction;

from a position B located one kilometre further along the road, the observer measures an azimuth 45°. To calculate CH, it is sufficient to solve the triangle ABC in order to calculate the CH distance knowing the two angles in A and B and the length of the baseline AB. We apply one of the relationships between angles and sides in a triangle.

a/sin(A) = B/sin(B) = C/sin(C), where (A), (B), (C) are the angles A, B, C of the triangle ABC.

So we have: a/sin(30°) = 1 km/sin(C) where (C) = 180° - ((A)+(B)) = 180° -165° = 15°, and therefore

a = sin(30°)/sin(15°.

But CH = a.sin(B) = sin(45°), and therefore

CH = 1366 m

Diurnal parallax and horizontal parallax

We saw previously that triangulation and parallax use the same principle to determine the distance to a remote object without having to go there and without measuring the distance to the object directly. It is important to note that the measuring accuracy depends on the length of the baseline. It is necessary to be able to measure the angles with sufficient precision. For a celestial body not too far from the Earth, it is sufficient to move across the surface of the Earth - or better, to make two simultaneous observations from two distant places on the Earth's surface.

We notice that during the course of a day the daily rotation of the Earth around its axis moves each observer. This displacement modifies the angle at which we see a celestial body placed at a finite distance, compared to the angle of sight from the centre of the Earth. This is called the diurnal parallax which, for an observer at a given place, will vary during the day. The distance separating two positions of the observer can serve as "baseline". It is easily seen that maximum value of the baseline is determined by the terrestrial diameter.

The diurnal parallax has a maximum value: it is the "horizontal parallax" for a given object. It is reached by an object observed at the horizon. This value is the angular size of the Earth’s radius seen from the object.

Annual parallax

Since stars are very remote, terrestrial baselines are not large enough for triangulation. We must use the annual parallax (the angular size of the radius of the Earth's orbit seen from the star), i.e. we observe the change in the apparent direction of the star from various positions of the Earth's orbit. The diameter of the Earth's orbit is about 300 million kilometres. If the annual parallax is one second of arc, we say that the star is at a distance of one parsec from the Earth. Very few stars have a measurable parallax. Astrometric satellites (Hipparcos in the past, Gaia in the future), by improving the accuracy of parallax measurements, make it possible to obtain the distances of many more stars than is possible from ground-based observatories.

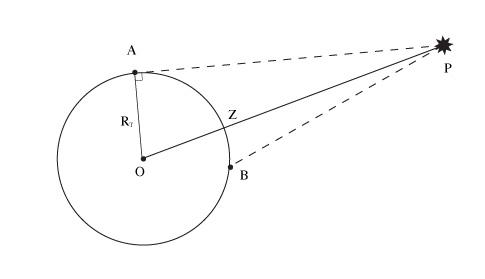
Measurement of a star's distance from the annual parallax due to the motion of the Earth around the Sun

This measurement also relies on triangulation and parallax but a large baseline is obtained by making the observations at a six-monthly intervals. Parallax measurements are accurate for nearby stars but not for distant stars. The distances of very remote stars are estimated using statistics, photometry and spectroscopy.

Parallax and the Earth-Sun distance

Having seen how astronomers measure the distances to planets and to stars, how can we measure the entire solar system? How can observations of the transit of Venus give us the distance from Earth to Venus?

In order to understand, let us see how we can measure the parallax of a given planet. It was realised that it was necessary to measure an angle of sight of a celestial body compared to a fixed direction, known by two observers, separated by a distance and not in contact. This fixed direction can be provided by a star located in the sky near to the body of which one wants to measure the distance, but sufficiently far from Earth to be regarded as being at infinity. In other words, its parallax should be considered as zero: whatever place on the Earth it is observed, we always see it in the same direction. So it is possible to use stars for which the diurnal parallax is negligible. This method was applied to the planet Mars as early as the 17th century but the measurement of star directions was difficult and an easier method was looked for. The planet Venus, passing regularly in front of the Sun, brought the solution. At the time of such a transit, the solar disc is a reference against which Venus appears at different places for different observers. It depends on the principle of parallax.

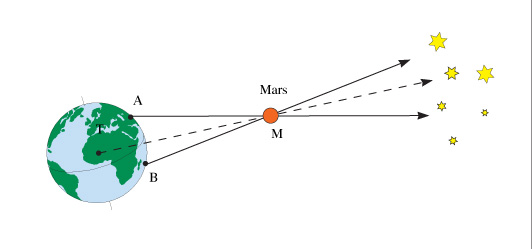
Case of Mars: the planet appears in front of different stars according to the observers' locations

For Mars, only the parallax principle and a calculation using a known baseline (determined by the separation of the observers) are needed to estimate the distance from Earth to Mars.

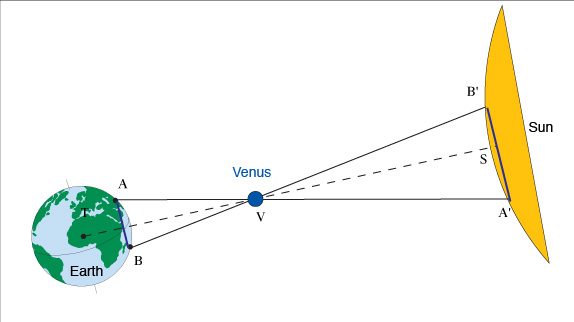
Case of Venus: the projection of the planet's dark disc on the solar disc at the time of a transit differs for two terrestrial observers.

For Venus, the Sun is used as a reference to calculate the parallax. However, there is an important difference from the calculation of Mars’ parallax since the Sun is at a finite distance and itself has a parallax. Thus we need to know the ratio of the distances from the Sun to Venus and to the Earth. That is provided by Kepler's laws. We know the distance AB, the angle at V (from observation) as well as ratio VA/VA' (by Kepler's third law); then we deduce VT, VS and TS and hence the Earth-Sun distance and the astronomical unit. The problem is complicated owing to the fact that A and B are moving due to the rotation of the Earth on its axis, and also T and V are moving due to the orbiting of the Earth and Venus around the Sun.

Distances in the solar system and Kepler's third law

The parallax principle is not sufficient to determine all the distances in the solar system. Only the planets Mars and Venus and asteroids like Eros that pass close to the Earth are accessible. The Sun and the other planets are too distant but Kepler's laws allow the problem to be solved.

Kepler's first law states that the orbits of planets around the Sun are ellipses. We need to use it because the distances Earth-Venus and Earth-Sun vary with time according to the position of these planets in their orbit.

Kepler's second law is the law of equal areas. It simply indicates that the planets go more quickly around their orbit when they are close to the Sun. We will use this law for the analysis of the transit observations for which we need to know the apparent angular velocity of Venus across the solar disc.

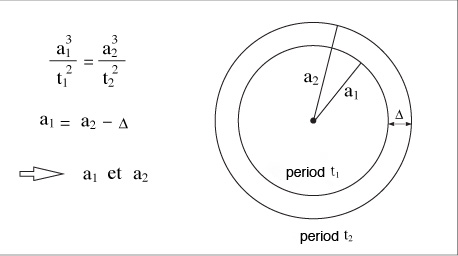
Kepler's third law provides us with the relationship between the distances from the Sun to all the planets. Knowing only one distance in the solar system, we can calculate all the others. It is stated as follows: the ratio a³/T² is constant for all planets of the solar system where a is the semi-major axis of an orbit and T the period of revolution around the Sun. The figure below shows what happens if the orbits are considered as circles, knowing the distance Δ and the period of revolution t₁ and t₂.

Kepler's Third Law

Kepler's first law states that the orbits of the planets are ellipses. It is not possible to say that the distances Earth-Sun and Venus-Sun may be taken identical to the semi-major axis a_T and a_V of the orbits of the Earth and Venus. Knowing the semi-major axis "a", we can calculate the distance Earth-planet (names radius-vector) "r_P" by using the formula: r_P = a (1 - e cos E) where e is the eccentricity of the ellipse and E a parameter giving the position of the planet in its orbit (the parameter is called "the eccentric anomaly" ) .

Conclusions

The parallax principle and Kepler's laws (discovered by analysing observations of the positions of the planets over a long time) are sufficient to allow us to measure the distance from Earth to Venus and hence all the distances of the planets from the Sun. Since the distance from Earth to the Sun is the baseline for calculating the distances to nearby stars, we can now measure the universe.

Go to the corresponding Brief InfoSheet

Back to the List of Extended InfoSheets.