The Venus Transit 2004
... Brief InfoSheet G4
Distances in the Solar System: parallax and Kepler's laws
| | How can we measure the size of the Earth, the distance to the planets and to the stars, and eventually understand the actual motions of objects in space? By using parallaxes ! By measuring the difference in the viewing angles of a given object as observed by two persons far from each other, one can relate the distance of the object to the distance between the two observers. On Earth, the method is used to measure the distance to remote places without going there: it is called triangulation . To calculate the distance from the Earth to a celestial body, one can proceed in a similar way. From two places on Earth, we can measure the angle of sight of a star and, knowing the length of the baseline, we can calculate the distance |
Of course, the measuring accuracy depends on the length of the baseline. It is necessary to be able to measure the angles with sufficient precision. For a celestial body not too far from the Earth, it is sufficient to move across the surface of the Earth - or better, to make two simultaneous observations from two distant places on the Earth's surface. This isn't enough however for even the closest of the stars.
We have then to rely on the annual parralax, i.e. we observe the change in the apparent direction of the star from various positions of the Earth's orbit. The diameter of the Earth's orbit is about 300 million kilometres. If the annual parallax is one second of arc, we say that the star is at a distance of one parsec from the Earth. Very few stars have a measurable parallax. Astrometric satellites (Hipparcos in the past, Gaia in the future), by improving the accuracy of parallax measurements, make it possible to obtain the distances of many more stars than is possible from ground-based observatories.
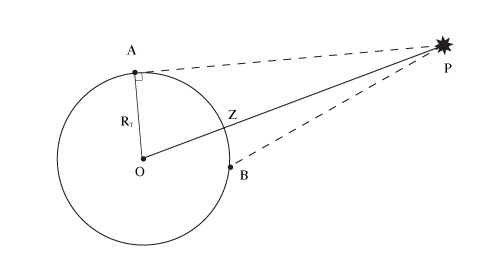
It is also possible to use the parallax effect to measure the distance to planets. To do this, one measures the angle of sight of a celestial body compared to a fixed direction, known by two observers, separated by a distance and not in contact. This fixed direction can be provided by a star located in the sky near to the body of which one wants to measure the distance, but sufficiently far from Earth to be regarded as being at infinity. This method was applied to the planet Mars as early as the 17th century but the measurement of star directions was difficult and an easier method was looked for. The planet Venus, passing regularly in front of the Sun, brought the solution. At the time of such a transit, the solar disc is a reference against which Venus appears at different places for different observers. It depends on the principle of parallax.
The parallax principle is not sufficient to determine all the distances in the solar system. Only the planets Mars and Venus and asteroids like Eros that pass close to the Earth are accessible. But one can rely on Kepler's laws provides us with a relationship between the distances from the Sun to all the planets. Knowing only one distance in the solar system, we can calculate all the others.
Want to know more?
This topic is discussed in a more detailed way in the associated Extended InfoSheet.
Back to the List of Brief InfoSheets.