



Next: Estimation
Up: Basic Concepts
Previous: Image sampling
Besides gross errors which are discussed in Section 2.2.1
the two main sources of noise in a frame come from the detector system
N and from photon shot-noise of the image intensity I
(see Equation 2.1).
It is assumed that the digitalization is done with sufficiently high
resolution to resolve the noise.
If not, the quantization of output values gives raise to additional noise
and errors.
A large number of independent noise sources from different electronics
components normally contributes to the system noise of a detector.
Using the central limit theorem, the total noise can be approximated by
a Gaussian or normal distribution which has the frequency function :
![\begin{displaymath}P_G(x;\mu,\sigma) = \frac{1}{\sigma\sqrt{2\pi}}
\exp \left( -\frac{1}{2} \left[ \frac{x-\mu}{\sigma} \right]^2
\right)
\end{displaymath}](img23.gif) |
(2.3) |
where 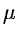 and
and  are mean and standard deviation, respectively.
The photon noise of a source is Poisson distributed with the probability
density PP for a given number of photons n :
are mean and standard deviation, respectively.
The photon noise of a source is Poisson distributed with the probability
density PP for a given number of photons n :
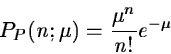 |
(2.4) |
where  is the mean intensity of the source.
It can be approximated with a Gaussian distribution when
is the mean intensity of the source.
It can be approximated with a Gaussian distribution when  becomes
large.
For photon counting devices the number of events is normally so small
that Equation 2.4 must be used while Gaussian approximation
often can be used for integrating systems (e.g. CCD's).
becomes
large.
For photon counting devices the number of events is normally so small
that Equation 2.4 must be used while Gaussian approximation
often can be used for integrating systems (e.g. CCD's).
In the statistical analysis of the probability distribution of data
several estimators based on moments are used.
The rth moment mr about the mean  and its dimensional
form
and its dimensional
form 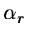 are defined as
are defined as
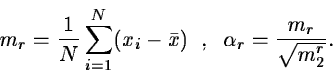 |
(2.5) |
The second moment is the variance while first is always zero.
The general shape of a distribution is characterized by the skewness
which denotes its asymmetry (i.e. its third moment  )
and
the kurtosis showing how peaked it is
(i.e. its fourth moment
)
and
the kurtosis showing how peaked it is
(i.e. its fourth moment  ).
For a normal distribution, these moments are
).
For a normal distribution, these moments are
 and
and
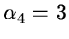 while for a Poisson distribution are
while for a Poisson distribution are
 and
and
 .
Besides these moments other estimators are used to describe a distribution
e.g. median and mode.
The median of a distribution is defined as the value which has
equally many values above and below it while a mode is the local
maximum of the probability density function.
.
Besides these moments other estimators are used to describe a distribution
e.g. median and mode.
The median of a distribution is defined as the value which has
equally many values above and below it while a mode is the local
maximum of the probability density function.




Next: Estimation
Up: Basic Concepts
Previous: Image sampling
Petra Nass
1999-06-15
![\begin{displaymath}P_G(x;\mu,\sigma) = \frac{1}{\sigma\sqrt{2\pi}}
\exp \left( -\frac{1}{2} \left[ \frac{x-\mu}{\sigma} \right]^2
\right)
\end{displaymath}](img23.gif)
![]() and its dimensional
form
and its dimensional
form ![]() are defined as
are defined as