



Next: Raw to Calibrated Data
Up: Basic Concepts
Previous: Noise distributions
Estimation
A number of different statistical methods are used for estimating parameters
from a data set.
The most commonly used one is the least squares method which estimates a
parameter 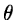 by minimizing the function :
by minimizing the function :
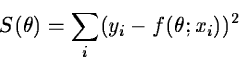 |
(2.6) |
where y is the dependent and x the independent variables while
f is a given function.
Equation 2.6 can be expanded to more parameters if needed.
For linear functions f an analytic solution can be derived whereas
an iteration scheme must be applied for most non-linear cases.
Several conditions must be fulfilled for the method to give a reliable
estimate of 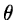 .
The most important assumptions are that the errors in the dependent variable
are normal distributed, the variance is homogeneous, and the independent
variables have no errors and are uncorrelated.
.
The most important assumptions are that the errors in the dependent variable
are normal distributed, the variance is homogeneous, and the independent
variables have no errors and are uncorrelated.
The other main technique for parameter estimation is the maximum likelihood
method where the joint probability of the parameter 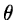 :
:
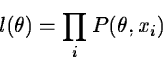 |
(2.7) |
is maximized.
In Equation 2.7, P denotes the probability density of
the individual data sets.
Normally, the logarithm likelihood
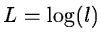 is used to simplify
the maximization procedure.
This method can be used for any given distribution.
For a normal distribution the two methods will give the same result.
is used to simplify
the maximization procedure.
This method can be used for any given distribution.
For a normal distribution the two methods will give the same result.




Next: Raw to Calibrated Data
Up: Basic Concepts
Previous: Noise distributions
Petra Nass
1999-06-15
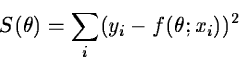
![]() :
: