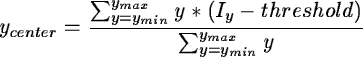Next: Removal of particle hits
Up: Echelle Spectra
Previous: General Description
Order Definition
The dispersion relation is defined by the following
equations:
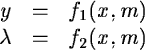 |
(7.1) |
The first of the equations 7.1 defines the position of the
spectral orders, m, in the raw image, while the second equation
gives, for each order, the dispersion relation in one dimension. The
mapping between the spaces
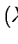 and (x,y) is separated into
two different equations; the first one will be discussed in this
Section, while the description of the second equation will be
postponed to Section 7.6.
and (x,y) is separated into
two different equations; the first one will be discussed in this
Section, while the description of the second equation will be
postponed to Section 7.6.
The function f1 is approximated by a polynomial of the form
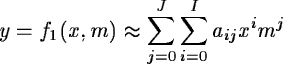 |
(7.2) |
where the coefficients aij are computed using least squares
techniques on a grid
(xk, yk), i.e. sample number and line number
of points located within the spectral orders of the image. These
points in the grid are found automatically by an order-following
algorithm, normally using the FLAT or STD image.
- A first guess of the position
of the orders is found on a trace perpendicular to the dispersion
direction done in the middle of the flat field image, in this way we define
the set of points
(x0,y0m), m being the relative order number.
- For each order, the order-following algorithm finds the series of
points located on the order at
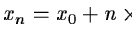 for points on the
right half of the order, and at
for points on the
right half of the order, and at
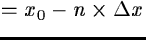 for points
on the left half of the order,
for points
on the left half of the order,
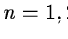 integer and
integer and  is
the step of the grid.
is
the step of the grid.
This set of points forms the basic grid with the geometric positions of the
orders. Typical values of the standard deviation of the residuals of this
approximation are about 0.3 to 0.1 pixel.
It is worth mentioning here that the order following algorithm finds
the center of the orders by taking the middle point with respect to the edges
of the orders. The edges of the orders are detected automatically by
thresholding the order profiles, perpendicular to the dispersion direction;
the level of the threshold is a function of the signal in the order.
The command DEFINE/ECHELLE performs the automatic order detection.
An alternative method is available, based on the Hough transform to perform
the order detection and involving a tracing algorithm able to estimate an
optimal threshold for each order independently.
The order definition is performed as
follows:
- A preprocessing of the frame is performed, including a median filtering
(radx,y=2,1) to remove hot pixels and bad rows from the image. Then the
background value is measured in the central area of the image
and subtracted. This preprocessing assumes that the
defaults are small enough to be corrected by a simple median filtering
and that the interorder background is basically constant all over the image.
If the above conditions are not respected, the frame must be processed by
the user. The echelle command BACKGROUND/SMOOTH enables
performance of a background correction at this early stage of the
calibration.
- A first guess of the position and the slope of the orders is found
by processing the Hough transform of a subset of columns of the input
image. The order detection by Hough transform is described in
(Ballester, 1994).
- For each order, an initial threshold is estimated by measuring the
pixel values in the middle of the order. The order following algorithm
finds the series of points located on the order at regular steps on
the grid, as describd above. The threshold is optimised in order to
follow the order on the longest possible distance. If the trace of the
order is lost, the algorithm extrapolates linearly the positions and
attempts to skip the gap.
- For each position, the center of the order is
defined as the first moment of the pixel values above the threshold:
This algorithm is implemented in the command DEFINE/HOUGH. The
algorithm can run in a fully automatic mode (no parameters
are required apart from the name of the input frame).
It is also possible to set the following parameters
to enforce a given solution:
- numbers of orders to be detected.
- half-width of orders
- threshold
A practical decription of the way to use this algorithm and to optimise the
parameters is described in the Appendix D




Next: Removal of particle hits
Up: Echelle Spectra
Previous: General Description
Petra Nass
1999-06-15
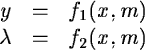
 is
the step of the grid.
is
the step of the grid.