Next: Analysis of Results
Up: Extraction of Information
Previous: Search Algorithms
The final step in data reduction is the extraction of astrophysical
parameters from the data. This is often done by fitting a
parameterized model of the objects to the data by means of least
squares and maximum likelihood methods (see Section 2.1.3). The
correct weighting of data is important in order to use all information
in the image and minimize the effects of noise on the final
parameters. For stellar images or line profiles, either analytical
functions (e.g. weighted Lorentzian-Gaussian profiles) or empirical
models of the PSF are used to obtain flux and shape parameters. Very
elaborate models may be applied to more complex objects such as
galaxies where the flux are decomposed in a set of different
components e.g. bulge, disk, bar and spiral.
When a set of objects have similar features and their relative shifts should
be determined, the correlation between them and a template object Tis analyzed using the cross-correlation function :
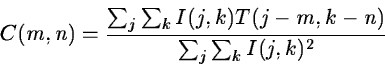 |
(2.31) |
where I is the object. Since this function is 1 for a perfect match
between object and template, the maximum value will indicate how
similar the objects are. The location of the main peak gives the
translation and is used in spectroscopy to determine radial velocities
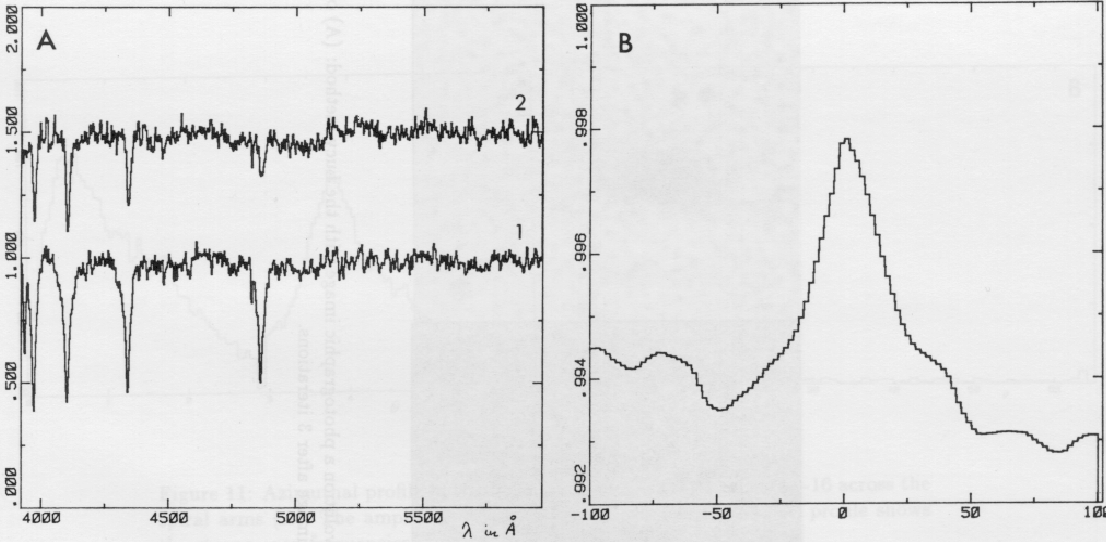
of stars. This is shown in Figure 2.12 where the
normalized spectra of two early type stars are cross-correlated.
Since only the spectral lines should be used, it is important to
subtract or normalize the continuum to avoid interference from it.
Figure 2.12:
Two normalized early type spectra used as template (A1) and
object (A2) yield the cross-correlation function (B).
 |




Next: Analysis of Results
Up: Extraction of Information
Previous: Search Algorithms
Petra Nass
1999-06-15