A general characterization of free convection at a surface of characteristic length L is given by the Raleigh number:
At low Raleigh numbers the flow is laminar,
although it may be unstable, until a transition at
to a fully turbulent regime.
Let us consider a simple situation in which
the air volume inside the dome enclosure
sketched in fig. 
is affected by free convection generated
by temperature differences between air and the floor of the dome.
The floor-air temperature difference will generate a system of
convection cells by which the heat is carried in the dome inner air
volume.
Since the flow conditions around a telescope are generally
too complex to hope to come
to rigorous modelisations of the areas interested by the seeing
effect, it will be of interest to understand the similarity
that rule the effect
of changes of one or more parameters on the seeing,
thereby deriving the criteria for interpreting the data obtained from
mirrors and telescopes of different scales and conditions.
In an extreme simplification we will consider the height from the
floor as the only geometrical parameter.
Mean statistical values, may then be obtained through similarity
theory (cf. section 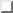). Following [Wyngaard],
we take as scaling variables
of the free convection field from a plane horizontal surface
, q
and z. There is no stability parameter and dimensional
reasoning leads then to
where b is a constant. Rearranging gives:
which, within the constant factor, is equation ()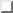
which had been derived for the unstable limit conditions
of a turbulent boundary flow.
Equation (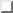) is a convenient expression to derive
a relationship of the integrated seeing 
with the flow scaling variables.
Noting that g and T, as well as air density and specific
heat are not scalable, and assuming further that the height dependency
will be constant through all scales, the scales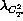 
and 
of seeing
are related to the scale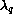 
of surface flux (the normalized
heat transfer rate) as
and, recalling equation (),
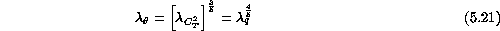
Noting that q is a likely function of temperature difference and upward flow speed, dimensional analysis gives:
Different expressions, depending on the particular conditions, are proposed to link the average value of flow speed in free convection. We will here take the simplest one:
Thus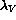 
is approximately:
One gets:
and finally
While this relationship is derived from dimensional reasoning,
we note that the exponent of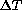 
in equation ()
obtained from experiments of free convection on a horizontal
surface actually varies from 1.25 to 1.6 depending on particular
conditions. The exponents given by textbooks
for free convection at
a horizontal plate are respectively 1.33
(laminar flow) and 1.25 (turbulent flow).
Equations () and ()
become in that case respectively:
[Giovannoni] gives also the experimental value of 1.6 for the case in which laminar free convection is influenced by an ambient stable stratification. This gives:
