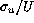The night-time surface layer is affected the radiative cooling of the ground which creates a thermally stable turbulent air layer. Simulation of turbulent flows at reduced scales must be based on strict similarity rules. The analysis of turbulent flow parameters allows the deductions of non-dimensional numbers which have to be respected in order that the flow in the wind tunnel correctly represents the real turbulent flow.
For an isothermal flow, the following three rules are sufficient to ensure similarity between two turbulent flows:
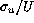has to be the same in
model and reality.
and the flow speed 
m/s.
When the turbulence is influenced by the thermal stratification, similarity of the flow requires additional conditions. If the flow speed is weak, the flow interacts with the thermal stratification and the result could be a slope-wind. In this case, similarity of a suitable stability parameter (such as the Richardson number or the Monin-Obukhov length) as well as of thermal air expansion are required. The analysis of similarity of such thermal winds is quite complex (see for instance [Hertig 86]) and leads to the requirements of a scale of about 1/2000 to 1/5000 depending on surface roughness ([Hertig 91]). Since this scale does not allow the correct simulation of turbulence spectra, it will not be possible to simulate seeing effects in these conditions.
In stronger winds the thermal stratification does no longer drive the flow but still affects the turbulence. The similarity of thermal air expansion can be relaxed and the flow is only characterized by the thermal stability conditions. These can conveniently be represented by the Richardson number:
Therefore for a correct simulation the scales (ratios of quantities between model and full scale conditions) of geometry, speed and temperature deviations shall be in the following relationship:
The graph in fig. 
gives the temperature scale
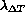as a function of the speed scale 
for different geometric scales 
. With a geometric scale of
1/200 and a speed reduction by a factor 2 or 4, sufficient to
maintain a turbulent flow, the scale of
temperature deviations in the wind tunnel with respect to full scale
will be respectively 50 and 12.5 .
For the presumed full scale temperature deviations of 1 to 3K, these
distorted temperature scales are indeed feasible in the wind tunnel.
It is therefore possible to simulate in the wind tunnel both
mechanical and thermal parameters of turbulence.
Figure: Required
scale of temperature deviations 
as a function of the speed scale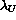 
for different geometric scales 
.
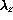The corresponding scaling of seeing can be conveniently derived from
equation () which parameterizes thermal turbulence in the
near-ground layer:
Thus the scaling factor for 
between model and full scale
conditions will be:
We can assume further that the temperature profiles are self-preserving for a same Richardson number, e.g.:
where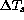 
is the bulk air-surface temperature difference and
the normalized temperature profile for a unit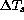 
.
Recalling equations () and (), we obtain for
the seeing FWHM along a vertical direction:
where B is defined as:
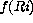shall be identical in both full and test scales, while
the integral in equation ()
is proportional to the vertical geometrical
scale to the power 1/5.
The scaling factor between model and full scale
conditions for seeing is then:
Summarizing, this scaling relationship will be valid and applicable to reduce scale tests provided that:
