

The Venus Transit 2004
... Educational Sheet 5
Approximated method for the calculation of the parallax
(with examples) [1]
Level: high school, highest degree
Objective: to understand the calculation of the parallax of the Sun, i.e. the calculation of the distance Earth-Sun from the observation of the transit of Venus from two observations of the transit from two different place on Earth
Assumptions: we present a simplified method since the direct complete calculation of the parallax is impossible without several iteration. We will suppose as known several parameters of the motion of the Earth and Venus around the Sun. The observations must be simultaneous.
Material required: hand calculator
Background: students must have a basic knowledge on :
- angles, trigonometry and vectors
- motion of the Earth and Venus
- laws of Kepler
- the ellipse
- the sphere
Introduction
In this note we present a simplified calculation for the average equatorial parallax of the Sun. The simplification is done at the price of an important observational constraint. We suppose that we have two simultaneous observations which give the distance between the two apparent centres of the planet Venus on the solar disc. We indicate the adopted approximations and simplifications.
Hypothesis
Consider two observing sites M 1 and M 2 , sufficiently far apart; the two observers note at the same time T the position of the apparent centre of the planet Venus in front of the solar disc. Using these two observations, it is possible to determine the distance between these two apparent Venus centres. The measurement of the separation of the centres, expressed in solar radii, allows the equatorial mean parallax of the Sun π 0 to be calculated. We will see that this measurement is far from being simple.
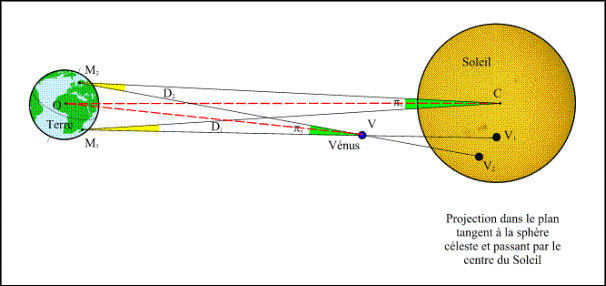
Figure 1. - Simultaneous observations of the transit of Venus from two sites
Let O be the centre of the Earth, C the centre of the Sun, V the centre of Venus and V 1 and V 2 the Venus centres on the solar disc seen respectively from the points M 1 and M 2. Let us note D 1 and D 2 the angles CM 1 V and CM 2 V formed by the directions of the lines joining the two observating sites to the centres of the Sun and Venus and note π S the angle subtended at the Sun by the segment M 1 M 2 and π v the angle subtended at Venus by the segment M 1 M 2. These two angles are the parallaxes of the Sun and Venus seen from the sites M 1 and M 2 (Figure 1).
If the two sites M 1 and M 2 are chosen at random within the zone of visibility of the transit, there is no reason for the four points M 1 , M 2 , V and C to be in the same plane. Thus, in general, the lines M 1 C and M 2 V are not in the same plane and do not intersect. One cannot assume the rules of plane geometry in Figure 1.
And the following relation : D 1 - D 2 = π S - π v is false . It is true only if the four points are coplanar.
On the contrary, the difference of the parallaxes is equal to the angular distance between the two apparent centres of Venus (Figure 2).
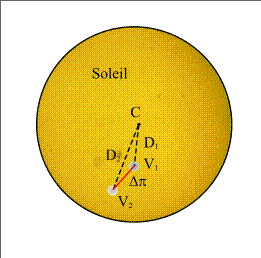
Figure 2. - Apparent positions of Venus on the solar disc.
It is easy to check that this difference is equal to D 2 - D 1 when the four points are coplanar i.e. when V 1 , V 2 and C are in line.
The value that the observers measure is thus the distance Δπ between the two apparent centres of Venus and the relation Δπ= π v -π S allow us to calculate the parallaxes.
To do that, we express the two parallaxes according to the distances between the centre of the Earth and the centre of Venus and the Sun. Let be R V the distance between the centre of the Sun and the centre of Venus and R T the distance between the centre of the Earth and the centre of the Sun so that the distance Venus-Earth equals R T - R V. To express this parallax we must also know the projection D of the distance between the two points M 1 M 2 on the normal plane to the Earth-Sun direction (Figure 3).
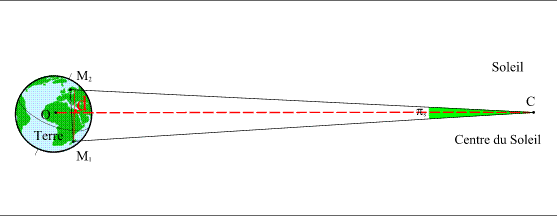
Figure 3. - Solar parallax related to the points M 1 et M 2.
As the Earth's radius and the separation of the two points are small compared to the Earth-Sun and Earth-Venus distances, the parallaxes are given by the following approximate formulas:
| |
Actually, the exact parallax are given by:
| |
Then we have the following relation:
| |
and
| |
or
| |
The measurement gives us the value D p in terms of the solar diameter and we must also measure the diameter of the Sun, because if the distance Earth-Sun is unknown, this diameter may not be calculated.
To know the solar parallax, it is thus necessary to know the ratio of the Sun-Earth and Sun-Venus distances. However this ratio can be calculated thanks to Kepler's laws.
The calculation of the ratio of the distances to the Sun using Kepler's laws
Kepler's first law says that the planets describe elliptic orbits around the Sun and that the Sun occupies one of the foci of these ellipses. At a given moment the radius vector R p joining the centre of the Sun to a planet p is calculated using the following formula: r p = a p ( 1 - e p cos E) (4)
Here a p is the semi-major axis of the ellipse, e p is the eccentricity of the ellipse and E is an angle called eccentric anomaly which makes it possible to locate the planet on its orbit.
Kepler's third law provides a relation between the semi-major axes of the orbits and the periods of revolution of the planets, thus for the same central body all the orbits of the planets which revolve around it obey the following relation :
| |
Kepler's laws thus describe the orbits of the solar system apart from a scale factor. Knowledge of the periods of revolution of the planets gives us the ratios of the semi-major axes, thus the ratio of the semi-major axis of the orbits of Venus and of the Earth is equal to :
| |
| and at any time T, the ratio of the radius vectors is equal to |
Thus Kepler's laws allow the ratio of the radius vectors for any time T to be calculated.
Our measurement allows us to calculate the value πS, it is thus appropriate now to pass from this value to the value of the mean equatorial parallax of the Sun π 0.
Calculation of the mean parallax of the Sun
The mean equatorial parallax of the Sun π 0 is defined as the angle subtended at the centre of the Sun by the equatorial radius of the Earth when the Sun is at one astronomical unit from the Earth.
We have thus the following relation :
| |
R being the Earth's equatorial radius and a the value of the astronomical unit.
However, equation (1) gives us the value of the solar parallax π S in terms of the R T Earth-Sun distance and projection d of the distance between the observing points onto the plane normal to the Earth-Sun direction.
It is sufficient to express this distance D in terms of the Earth's radius and the Earth-Sun distance in astronomical units to have a relation between π S and π 0.
| |
It only remains to calculate the ratio of D on R. The a/R T ratio is provided Kepler's law (cf. Eq. 4). However if we take the vector product of the two vectors 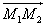 and
and  we obtain :
we obtain :
| |
However the product of the length of the first vector by the sine of the angle between the two vectors 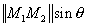 is equal to the distance d. In the same way the length of
is equal to the distance d. In the same way the length of  is equal to the distance R T (figure 4).
is equal to the distance R T (figure 4).
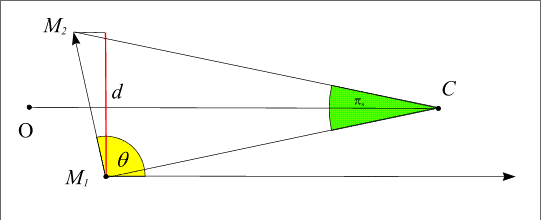
Figure 4. - The solar parallax in relation to the points M 1 et M 2.
Solving equation 10 gives us the value of d.
| |
Note : if the concept of vector product is not known, one can use the scalar product of the same vectors, so allowing the calculation of the cosine of the angle and then its sine using the relation : 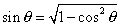 .
.
Description of this calculation :
This calculation needs the Cartesian co-ordinates of the two points M 1 and M 2 and of the centre of the Sun C in an orthogonal reference frame (O, x, y, z) with origin at the centre of the Earth. We will use the apparent geocentric equatorial reference frame for this calculation.
ThE reference frame is defined by the plane of the Earth's equator at the time T of the observation (plane Oxy) and by the direction of the northern celestial pole of the Earth's rotation axis (Oz). In this reference frame we can define a Cartesian reference frame (x, y, z) and a polar reference frame (α, δ, R) where the two angles are called "right ascension" and "declination" (Figure 5). We pass from one system to the other using the following relations :
| |
and the converse relations:
| |
The direction of axis Ox at the time T is the direction of the vernal equinox on that date.
The ephemerides (i.e. Kepler's laws) give us the geocentric equatorial coordinates of the centre of the Sun (α, δ); the distance is not know but is not important because the vector  may be replaced by its unit vector in equation 11.
may be replaced by its unit vector in equation 11.
A more complicated problem is the determination of the cartesian coordinates of the points M 1 et M 2 in this equatorial frame.
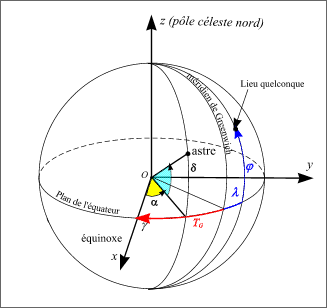
Figure 5. - Geocentric equatorial coordinates.
The position of a point on the surface of the Earth is given by its latitude and longitude (geographic); latitude is referred to the terrestrial equator, so it is like the ideclination angle. Longitude is referred to a zero meridian (the Greenwich meridian), so that it is similar to right ascension, but with a different origin from that of the celestial equatorial coordinates. Then we need to know for each date the angle between the direction of the Ox axis and the direction of the projection of the zero meridian on the equatoral plane (cf. Figure 5). This angle is related to the Earth's rotation: it is called the "sidereal time" of the Greenwich meridian and it increases by 360° during 23h 56m 4s (the sidereal revolution of the Earth).
Thus, it is sufficient to know the sidereal time of Greenwich T G at 0h UTC on the day of the transit in order to know the sidereal time of Greenwich at any time t, and then the sidereal time of any point on Earth having a longitude λ.
| |
We pass from Greenwich sideral time to the sidereal time of the site M having longitude λ, by adding or substracting its longitude.
Beware! Sidereal time increases going eastwards from the Greenwich meridian; it is thus necessary to pay attention to the sign convention used for longitudes.
If the longitudes are counted negatively towards east then the relation linking local sidereal time to the meridian line of the site of longitude λ and sidereal time with the Greenwich meridian is as follows: T λ = T G - λ (15)
Note that the two angles must be expressed in the same units (degrees or hours). Then the cartesian coordinates of a point M 1 with geographical coordinates (φ 1 , λ 1 ) at time t are given by:
| |
The length ||M 1 M 2 || of the vector 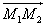 (its modulus) and its coordinates (X, Y, Z) are given by :
(its modulus) and its coordinates (X, Y, Z) are given by :
| |
The coordinates of the vector  of the direction "centre of the Earth - Sun" is given by :
of the direction "centre of the Earth - Sun" is given by :
| |
The vector product 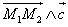 and its modulus are then :
and its modulus are then :
| |
and finally, using equation (11), we get :
| |
And the mean equatorial parallax is given (following Eq. (9)) by :
| |
Numerical application
Example 1: observation of the positions of the centres
We will take as an example the observation made at Antananarivo (Madagascar) and at Helsinki (Finland) at the time t=8h 30min on June 8, 2004.
The geographic coordinates of Antananarivo are :
Latitude :18° 52' south, longitude : 47° 30' east then φ 1 = -18.866667° and λ 1 = -47.5°.
The geographic coordinates of Helsinki are :
Latitude :60° 8' north, longitude : 25° 3' east, then φ 2 = 60.133333° and λ 2 = -25.05°.
The geocentric equatorial coordinates of the Sun at 8h 30m UTC are provided by the ephemerides:
Right ascension of the Sun α s = 76deg; 49' 36.493"
Declination of the Sun δ s = +22° 53' 16.237"
The sidereal time at Greenwich at a time t in UTC is provided by the following formula :
T G (t UTC) = 17h 6m 51,31s + 1,002737908 t
Then the sidereal time at Greenwich at 8h 30min is equal to :
T G = 17h 6m 51,31s + 8h 31m 23,78s = 25h 38m 15,09s = 1h 38m 15,09s
It is necessary to convert to degrees before calculating the local sidereal time for the two cities.
T G = 1h 38m 15.09s = 24.562875°.
From this, we deduce the local sidereal time at 8h 30m at Antananarivo :
Tλ 1 = 24.562875 - (-47.5°) = 72.062875°
And the sidereal local time at 8h 30m at Helsinki is :
Tλ 2 = 24.562875 - (-25.05°) = 49.612875°
We deduce the cartesian equatorial coordinates for these two places:
-
Antananarivo :

-
Helsinki :

The coordinates of the unit vector  of the Earth-Sun direction are obtained through equation 18 :
of the Earth-Sun direction are obtained through equation 18 :
 |
The vector 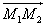 has coordinates :
has coordinates :
 |
Formula 20 allows us to calculate the value of d :
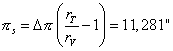 |
The ephemerides give us the ratio between the radii vectors and the ratio between the Earth-Sun distance and the semi-major axis of the orbit of the Earth on the given date : r T / r V = 1.397795 and r T / a = 1.015087
Now, we just have to make an assumption about the measured values, i.e. about Δπ and about the solar diameter : we will suppose that Δπ= 0.015 φ and φ = 31.51'. That gives the value of Δπ : 28.359"
Equation 3 gives us the value of the solar parallax :
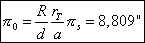 |
And equation 21 gives us the value of the mean equatorial parallax :
 |
The value that we find is relatively close to reality, but it depends only on the separation of the apparent centres of Venus on the solar disc and on the size of the solar diameter. The apparent size of the solar diameter can be measured with a good precision; on the other hand the separation of the apparent centres of Venus is not obvious. On a traditional photographic exposure where the apparent diameter is around 20mm, the distance between the centres is then about 0.3mm and a precision of one in a thousand corresponds to a measurement of 0.02mm.
In the preceding discussion we ignored a number of difficulties in order to simplify the problem. Below is a list of the complications which arise if we want to make a rigorous calculation:
- Because of mutual disturbances, the orbits of the planets do not follow Kepler's laws (valid only for two bodies) but more complex trajectories.
- It is not the Earth which has a quasi-elliptic orbit around the Sun but the barycentre of the Earth-Moon system.
- Following the movement of the Earth's rotation axis (precession and nutation), the origin Ox of the equatorial reference frame varies with time.
- Since light travels at a finite speed, the positions of the Sun and Venus at a given time t are not geometric positions but the positions of two bodies at the time t - τ p , τ p being the time used by the light to go from each body to the Earth. Since these distances are not supposed to be known, it is necessary to iterate the calculations to take it into account.
Calculation of the parallax from the times of the contacts
or from the duration of the transit
We saw, in InfoSheet n° 0 4b, that there are two simplified formulas allowing the direct calculation of the parallax by comparing the times of the same contact seen from two different places (Delisle method) or by comparing the duration of the transit observed from two different places (Halley method).
We will study simultaneouly these two aspects from the preceeding numerical example.
The mean equatorial solar parallax π 0 is obtained by comparing two identical contacts using the following simplified formula (cf. formula 16 of the sheet n° 0 4b) :
 (22) (22) |
If we neglect the uncertainties and the errors, then the formula becomes:
 (23) (23) |
Similarly, the mean equatorial solar parallax is obtained by comparing two identical durations using the following formula (cf. equation 21 of the Sheet n° 0 4b) :
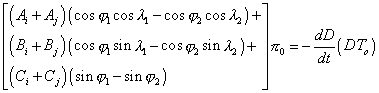 (24) (24) |
i and j are the indices related to the same contacts: i = 1, j = 4 for the exterior contacts and i = 2, j = 3 for the interior contacts.
The coefficients A, B, C and the term dD/dt are calculated for each contact and are given by the following table :
| Description of the contact | A | B | C | dD/dt "/min |
| First exterior contact (index 1) | 2.2606 | -0.0194 | 1.0110 | -3.0846 |
| First interior contact (index 2) | 2.1970 | 0.2237 | 1.1206 | -2.9394 |
| Last interior contact (index 3) | -1.0929 | -1.1376 | 1.9090 | 2.9391 |
| Last exterior contact (index 4) | -0.9799 | -1.3390 | 1.8383 | 3.0842 |
Example 2: observation of the times of the contacts
We will take again the example of the same two places with the observational hypothesis as follows :
- City n°1 : Antananarivo (φ 1 = -18.866667° et λ 1 = -47.5°)
Date of the first observed internal contact (index 2) : t2 = 5h 35m 30s UTC.
Date of the last observed internal contact (index 3) : t3 = 11h 8m 4s UTC
Observed duration of the transit (internal): 5h 32m 34s. - City n°2 : Helsinki (φ 2 = 60.133333° et λ 2 = -25.05°)
Date of the first observed internal contact (index 2) : t2 = 5h 38m 38s UTC.
Date of the last observed internal contact (index 3) :t3 = 11h 2m 20s UTC
Observed duration of the transit (internal) : 5h 23m 42s.
In equations (22) and (23) the factors of the coefficients A, B, C are identical and may be calculated separately:
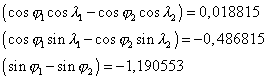 |
Calculation of the parallax using the first contacts :
The differences between the dates of the first interior contacts is -3m 8s (-3.1333m), and the use of the values of the coefficients A 2 , B 2 , C 2 and dD/dt in the formula (22) will provide us the following equation :
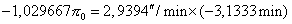 |
That gives π 0 =8.945'.
Calculation of the parallax using the duration of the interior transits
The difference in duration of the interior transits is 8m 52s (8.866m), and the use of the values of the coefficients A 2 , B 2 , C 2 , A 3 , B 3 , C 3 and dD/dt in equation (23) provides us the following equation :
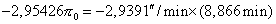 |
Note that it is the value
 |
and mainly its sign which may be used.
That gives π 0 =8.822'.
Let us remember that these methods are not completely accurate and we should use more complete formulas for the reduction of the observations.
[1] Written by P. Rocher (IMCCE)

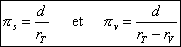 (1)
(1) 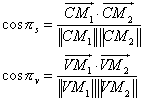
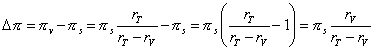 (2)
(2) 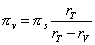
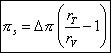 (3)
(3) 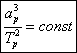 (5)
(5) 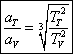 (6)
(6) 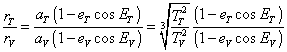 (7)
(7)  (8)
(8) 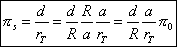 (9)
(9)  (10)
(10)  (11)
(11) 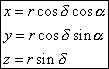 (12)
(12) 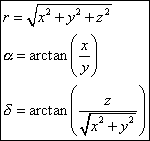 (13)
(13)  (14)
(14) 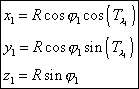 (16)
(16) 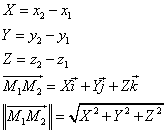 (17)
(17) 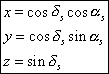 (18)
(18) 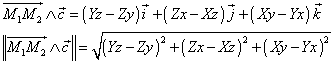 (19)
(19)  (20)
(20) 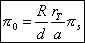 (21)
(21)