The Venus Transit 2004

... Educational Sheet 2

Appendix 3

Measuring distances by the triangulation method: how far is it?

You need an angle-measuring tool, a quadrant or a angle measurer or a theodolite used by surveyors.

You need also one or two poles, about as high as yourself and a tape measure.

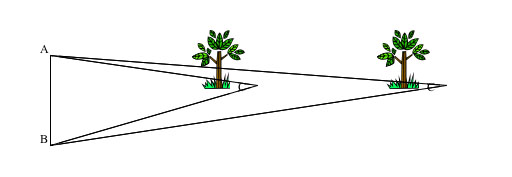
Here's how we might measure the distance of a tree, as in the situation that is sketched above. Imagine you can walk from A to B, but you can't reach the tree, for instance because there is a river between you and the tree. The trick is that you determine the shape and the dimensions of the triangle ABC (or ABC_). When you measure AB (the baseline) and the two angles BAC and ABC, the triangle is completely known. As you may see, when the tree is farther away (C_), the shape of the triangle becomes different.

But how can you determine this triangle in reality? First you establish a baseline and measure its length with the tape measure. The baseline runs between points A and B. Put your poles at A and B vertically into the ground, so you mark those places. Together with the tree at point C, the three points form a triangle.

We stand at point A and measure the angle BAC using an angle-measuring tool by looking at the tree and at the pole at B. Then we move to the point B and measure the angle ABC. Now we know the length of one side of the triangle - our baseline - plus the angles at which the other sides branch off from it. At this point, we can construct on paper a scale diagram to determine the distance of the tree (or we could use the rules of trigonometry). Using your ruler and the scale, you can easily calculate the distance from your baseline to the tree.

Questions:

1a. When you want to determine the distance of a remote object and the baseline stays the same, what are the consequences for the measurement of angles and the calculation of the distance?
Answer: The angles have to be measured much more accurately because a small change in angle makes a big difference to the distance.

1b. How can you overcome your problem?
Answer: In two ways: by making the baseline longer or by using a more accurate angle-measuring tool.

1c. Imagine you want to determine the distance to the Moon in this way. In this case you need a very long baseline. How long may it be? What will be the practical objection to using the method of triangulation in this case?
Answer: It will not be possible anymore to measure the angles BAC and ABC, because you can't see B from A and vice versa.

Conclusion:

Triangulation is possible only when the divergent vantage points are visible to each other. However, the triangulation method is used very much on the Earth by surveyors. It is no longer useful when the object is very far away, as celestial objects are. In that case another method is used, somewhat similar to the triangulation method; it is called the parallax method.

Back to EduSheet2.