

Venus Transit 2004
... Forms for Calculating the AU
by J.-E. Arlot, P. Rocher (IMCCE)
I.Introduction
On this page, we provide very simple formulae allowing to calculate an approximate value of the solar parallax from two observations made from two, geographically distant observing sites. Be careful - the choice of the observing site is important! The page about "Observing Partners" provides useful information about the choice of the two sites of observation
You will find below two types of formulae :
Formulae using the timing of two contacts of the same type between Venus and the Sun. Be careful, the two observations must concern the same type of contact, either the first external contact, the first internal contact, the last internal contact or the last external contact. This method requires a clock running in Universal Time in order to make the timings of the contacts on the same time scale to within one second of time. This method corresponds to Delisle’s method .
Formulae using the duration between two sets of the same type of contacts . With this method, we will take into account the duration of the transit of Venus in front of the Sun, measured between two sets of contacts of the same type, i.e., either between the two external contacts (which is difficult!), or between the two internal contacts. This method does not need to have the Universal Time scale available, since only the duration is needed. However, this method requires that both of the observing sites are able to observe both the beginning and the end of the transit. This method corresponds to Halley’s method .
Pre-calculated coefficients
In order to provide very simple formulae, we have pre-calculated the parameters A, B et C which do not depend on the positions of the observers but which take into account the motions of Venus and the Earth around the Sun and the rotation of the Earth around its axis. The parameter dD/dt represents the instantaneous variation of the distance from the center of Venus to the center of the Sun. Then, a calculation of triangulation is possible between the two observing sites, Venus and the Sun (even not in the same plane) and using Kepler’s Third Law to determinate the relationship between the Earth-Sun distance and the Venus-Sun distance.
| Description of the contact | A | B | C | dD/dt "/min |
| First external contact (index 1) | 2,2606 | -0,0194 | 1,0110 | -3,0846 |
| First internal contact (indice 2) | 2,1970 | 0,2237 | 1,1206 | -2,9394 |
| Last internal contact (index 3) | -1,0929 | -1,1376 | 1,9090 | 2,9391 |
| Last external contact (index 4) | -0,9799 | -1,3390 | 1,8383 | 3,0842 |
Table n°1
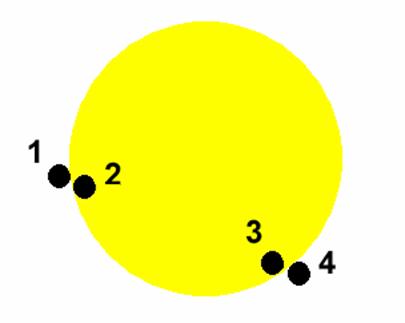
Successive contacts between Venus and the Sun
II Observation of the contacts
You need the following numerical data :
- latitudes and longitudes of the two observing sites ( l 1 , j 1 ; l 2 , j 2 )
- the timings of the contacts « i » (i=1, 2 , 3 or 4) observed at the sites 1 and 2 in the same time scale –referred to Universal Time- (t i,1 ; t i,2 )
The formula is as follows :
[A i (cos j 1 cos l 1 – cos j 2 cos l 2 ) + B i (cos j 1 sin l 1 – cos j 2 sin l 2 )
+ C i (sin j 1 – sin j 2 )] p 0 = – dD/dt (t i,1 – t i,2 )
To make the calculation, follow the calculation sheet “Delisle” below.
III Observation of the durations
You need the following numerical data :
- latitudes and longitudes of the two observing sites ( l 1 , j 1 ; l 2 , j 2 )
- the difference DT of the observed durations of the transit from the two observing sites (duration from site 1 – duration from site 2) corresponding to the contacts « i and j » (i,j=1,4 for the external contacts or 2,3 for the internal contacts) observed from the sites 1 and 2
- The formula is as follows :
[(Ai+Aj) (cos j 1 cos l 1 – cos j 2 cos l 2 )
+ (Bi+Bj) (cos j 1 sin l 1 – cos j 2 sin l 2 )
+ (Ci+Cj) (sin j 1 – sin j 2 )]. p 0
= – DT. dD/dt
To make the calculation, follow the calculation sheet “Halley” below.
Calculation sheet « Delisle » :
Calculation of the solar parallax using the observation of the contacts from two observing sites
You need the following numerical data :
- latitudes and longitudes of the two observing sites ( l 1 , j 1 ; l 2 , j 2 )
- the timings of the contacts « i » (i=1, 2 , 3 ou 4) observed at the sites 1 and 2 in the same time scale –referred to Universal Time- (t i,1 ; t i,2 )
Formula (F1) is as follows :
[A i (cos j 1 cos l 1 – cos j 2 cos l 2 )
+ B i (cos j 1 sin l 1 – cos j 2 sin l 2 )
+ C i (sin j 1 – sin j 2 )] p 0
= – dD/dt (t i,1 – t i,2 )
To make the calculation,please fill up the calculation sheet “Delisle” below. Attention, one sheet for two observations of the same contact « i »
Longitude of the observing site n°1 : l 1 =
(1) Calculate the cosine of l 1 : cos ( l 1 ) =
(2) Calculate the sine of l 1 : sin ( l 1 ) =
Latitude of the observing site n°1 : j 1 =
(3) Calculate the cosine of j 1 : cos ( j 1 ) =
(4) Calculate the sine of j 1 : sin ( j 1 ) =
Longitude of the observing site n°2 : l 2 =
(5) Calculate the cosine of l 2 : cos ( l 2 ) =
(6) Calculate the sine of l 2 : sin ( l 2 ) =
Latitude of the observing site n°2 : j 2 =
(7) Calculate the cosine of j 2 : cos ( j 2 ) =
(8) Calculate the sine of j 2 : sin ( j 2 ) =
(9) Calculate (cos j 1 cos l 1 ) = line (3) x line (1) =
(10) Calculate (cos j 2 cos l 2 ) = line (7) x line (5) =
(11) Calculate (cos j 1 cos l 1 – cos j 2 cos l 2 ) = line (9) – line (10) =
(12) Calculate (cos j 1 sin l 1 ) = line (3) x line (2) =
(13) Calculate (cos j 2 sin l 2 ) = line (7) x line (6) =
(14) Calculate (cos j 1 sin l 1 – cos j 2 sin l 2 ) = line (12) – line (13) =
(15) Calculate (sin j 1 - sin j 2 ) = line (4) – line (8) =
Value of the index i for this calculation =
(16) Determinate Ai from table n°1 =
(17) Determinate Bi from table n°1 =
(18) Determinate Ci from table n°1 =
Now, determination of the numerical value of the first member of equation (F1) :
(19) Calculate Ai x line (11) =
(20) Calculate Bi x line (14) =
(21) Calculate Ci x line (15) =
(22) Calculate the first member of (F1) :
line (19) + line (20) + line (21) =
(23) Observed timing of the contact « i » from site n°1 : t i,1 =
(24) Observed timing of the contact « i » from site n°2 : t i,2 =
(25) Difference between those two timings : (t i,1 – t i,2 ) =
(26) Convert this difference into minutes anf fraction of minute =
(27) Determinate dD/dt from table n°1 : dD/dt =
(28) Calculate the second member of equation (F1) :
line (27) x line (26) x (-1) =
(29) Calculate p 0 = line (28) / line (22) =
(30) Radius of the Earth = 6 378,1363 km
(31) Calculate now the astronomical unit :
AU = line (30) x 206265,806247 / line (29) =
You may make the calculation for each contact.
Calculation sheet « Halley » :
Calculation of the solar parallax from the observation of the duration of the transit from two different observing sites
You need the following numerical data :
- latitudes and longitudes of the two observing sites ( l 1 , j 1 ; l 2 , j 2 )
- the duration DT of the transit of Venus for each of the two sites 1 and 2 corresponding to external contacts (i=1, j=4) or internal (i=2, j=3)
- the difference between the durations DT observed from the two observing sites (duration site 1 – duration site 2) corresponding to the external contacts (i=1, j=4) or internal (i=2, j=3)
Formula (F2) is as follows :
[(Ai+Aj) (cos j 1 cos l 1 – cos j 2 cos l 2 )
+ (Bi+Bj) (cos j 1 sin l 1 – cos j 2 sin l 2 )
+ (Ci+Cj) (sin j 1 – sin j 2 )]. p 0
= – DT. dD/dt
Longitude of the observing site n°1 : l 1 =
(1) Calculate the cosine of l 1 : cos ( l 1 ) =
(2) Calculate the sine of l 1 : sin ( l 1 ) =
Latitude of the observing site n°1 : j 1 =
(3) Calculate the cosine of j 1 : cos ( j 1 ) =
(4) Calculate the sine of j 1 : sin ( j 1 ) =
Longitude of the observing site n°2 : l 2 =
(5) Calculate the cosine of l 2 : cos ( l 2 ) =
(6) Calculate the sine of l 2 : sin ( l 2 ) =
Latitude of the observing site n°2 : j 2 =
(7) Calculate the cosine of j 2 : cos ( j 2 ) =
(8) Calculate the sine of j 2 : sin ( j 2 ) =
(9) Calculate (cos j 1 cos l 1 ) = line (3) x line (1) =
(10) Calculate (cos j 2 cos l 2 ) = line (7) x line (5) =
(11) Calculate (cos j 1 cos l 1 – cos j 2 cos l 2 ) = line (9) – line (10) =
(12) Calculate (cos j 1 sin l 1 ) = line (3) x line (2) =
(13) Calculate (cos j 2 sin l 2 ) = line (7) x line (6) =
(14) Calculate (cos j 1 sin l 1 – cos j 2 sin l 2 ) = line (12) – line (13) =
(15) Calculate (sin j 1 - sin j 2 ) = line (4) – line (8) =
Value of the index i and j for the calculation : 1 and 4 for a duration calculated from the external contacts ; 2 and 3 from the internal contacts)
i =
j =
(16) Determinate Ai from table n°1 =
(17) Determinate Aj from table n°1 =
(18) Calculate Ai + Aj =
(19) Determinate Bi from table n°1 =
(20) Determinate Bj from table n°1 =
(21) Calculate Bi + Bj =
(22) Determinate Ci from table n°1 =
(23) Determinate Cj from table n°1 =
(24) Calculate Ci + Cj =
Now, determination of the numerical value of the first member of equation (F1) :
(25) Calculate (Ai+Aj) x line (11) =
(26) Calculate (Bi+Bj) x line (14) =
(27) Calculate (Ci+Cj) x line (15) =
(28) Calculate the first member of (F2) :
line (25) + line (26) + line (27) =
(29) Duration of the transit observed from site n°1 =
(30) Convert this duration into minutes anf fraction of minute =
(31) Duration of the transit observed from site n°2 =
(32) Convert this duration into minutes anf fraction of minute =
(33) Difference between the durations : DT = line (30) – line (32) =
(34) Determinate dD/dt from table n°1 : dD/dt =
(by averaging the absolute values of the beginning i and the end j)
(35) Calculate the second member of equation (F2) :
line (33) x line (34) x (-1) =
(choose the sign in order to have line (36) positive)
(36) Calculate p 0 = line (35) / line (28) =
(37) Radius of the Earth = 6 378,1363 km
(38) Calculate the astronomical unit :
AU = line (37) x 206265,806247 / line (36) =
Please be reminded that these methods are not completely accurate and that one must use more complicated formulae for a better reduction of the data. Even if your observations are perfect, you will get only an approximate value of the Astronomical Unit by using them. The error may reach 10 to 20 millios kilometres if the observing sites are badly chosen, e.g., by providing observed values from two sites that are too close to each other.
