The Venus Transit 2004
... Educational Sheet 3
How to Calculate the Earth-Sun distance
from the Transit of Venus [1]
Level: Some mathematical ability is required
Objectives:
- To measure the Earth-Sun distance using observations of the Transit of Venus from two places on the Earth lying on the same meridian. It is possible to calculate the Earth-Sun distance from observations taken from two places with different longitudes but the mathematics is much more difficult.
- To understand a very simplified version based on the first measurement carried out in 18th century. (The observational data from 1769 will be used to get a numerical result).
Assumptions:
In order to offer a method accessible to secondary school students we assume that:
- a) the two observing locations, their projections on the Sun's surface and the centre of the Earth, the Sun and Venus are in the same plane.
- b) the orbits of Venus and the Earth around the Sun are circular.
(Simple explanations of the assumptions are given by a three-dimensional model).
Background:
Having made the above assumptions, the students need to know only:
- Mathematical content
- The sum of the three angles of a triangle equals 180 degrees.
- Definition of sinus and tangent
- Direct proportions
- Pythagoras' theorem (optional)
- Astronomical content
Materials Needed:
- Ruler
- Calculator
Resources:
A three-dimensional model
Introduction:
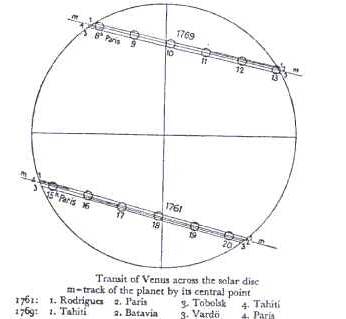
Sir Edmond Halley suggested campaigns to observe the transits of Venus in 1761 and 1769 and Jean-Nicolas Delisle gathered all the results together. We will use these observations to calculate the Earth-Sun distance by a simplified method for observers on the same meridian . Observers were located at latitudes as far away from one another as possible , to improve the accuracy of the calculations.

The method used here is a simplified version of the one Edmond Halley used in the 18th century
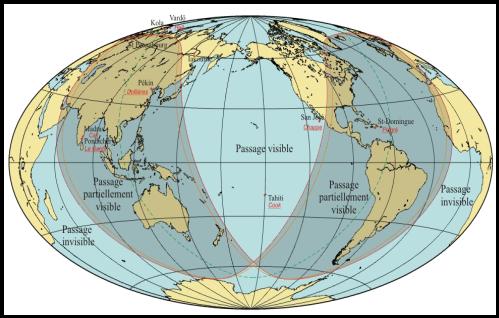
The selected observing sites were often in very remote places and journeys at that time were dangerous because of storms and wars between nations, as was the case in the Indian Ocean where England and France were fighting. It must be emphasized that the 1761 transit was the first occasion that a scientific campaign had been organised on an international basis and it involved more than 130 different expeditions all around the world. In 1769, there were observers at Pondichery in Madras , at St Domingo in the West Indies, at San José del Cabo in Baja California, at Hudson's Bay in Canada, at Papeete in Tahiti, at Vardö in Lapland, at Cajanebourg on the Kola Peninsula and at Iakoutsk in Siberia. Altogether there were 151 observers at 77 different locations. All the expeditions had different problems, some of them very challenging, and the results didn't always live up to expectations!
Observations from the Earth:
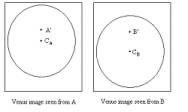
Let's consider two observers on the Earth situated at places A and B on the same longitude (meridian), but at very different latitudes. Venus is seen as a small disc on the face of the Sun at two different points A' and B'. This is because the lines of sight of A and B towards Venus are different.
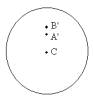
Putting the two observations together it is possible to measure the parallax displacement. After superimposing the two Sun centres at C, the separation of A' and B' is the distance between the two positions of Venus observed simultaneously from A and B.
If we observe the movement of Venus during the entire transit we can draw the locus of its positions during the complete observation. If we observe from places A and B we will get two parallel lines, one for each place. The separation of the lines is the parallax displacement Δβ.

Composite of several photos of the Mercury transit, 7 May 2003
How to measure the Earth-Sun distance
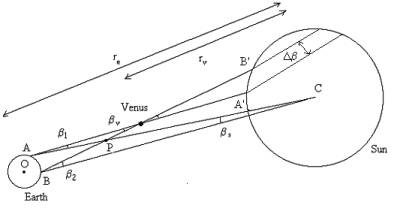
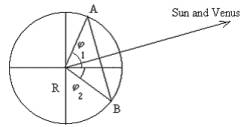
Let's consider the plane defined by three points: the Earth's centre O, the Sun's centre C and Venus' centre V. If the two observers are on the same meridian at places A and B, their images of Venus are at points A' and B' on the Sun's surface. (Actually the centres of the Earth, Venus and the Sun are not in the same plane as you can see in the model (link 1), but this assumption allows us to simplify the mathematical problem).
The triangles APV and BPC have the same exterior angles at P and since the sum of their angles is equal,
β v + β 1 = β s + &beta 2 ;
therefore
β v - β s = β 2 - β 1 = Δβ
where the angle Δβ measures the separation of the different positions of Venus's path over the face of the Sun. Rearranging the last equation gives
Δβ = β s ((β v / β s ) - 1)
Let's take r e as the Earth-Sun distance and r v as the Venus-Sun distance. Now Venus' parallax (link parallax definition) is β v = AB / (r e - r v ) and the Sun's parallax (link Sun definition) is β s = AB / r e , hence the quotient β v / β s = r e / (r e - r v ). Substituting this into the equation above gives
Δβ = β s ((r e / (r e - r v )) - 1) = β s r v / (r e - r v )
In particular, we can get the solar parallax
β s = Δβ ((r e / r v ) - 1)
Note that Δβ is the parallax displacement, that is to say the separation of the two lines.
We can calculate the ratio r v / r e using Kepler's Third Law as we know that the periods of revolution of Venus and of the Earth ar e 224.7 days and 365.25 days respectivel.
(r e / r v ) 3 = (365.25 / 224.7) 2
therefore
r e / r v = 1.38248
Using this result in the solar parallax relationship, we get
β s = Δβ ((r e / r v ) - 1) = Δβ (1.38248 - 1)
therefore
β s = 0.38248 Δβ
And finally, using the parallax definition (link 3), the distance from the Earth to the Sun r e is
r e = AB / &beta s ;
So we need to find the distance AB between the two observers and to measure Δβ from observational data of the transit.
The observations of 1769
In order to demonstrate how the results are calculated, we will use the observations of the 1769 campaign published in "A History of Astronomy" by A. Pannekoek. His book shows drawings and tables with the contact times recorded at various locations in 1761 and 1769. We will use the 1769 observations of Vardö (Lapland) and Papeete (Tahiti) for the demonstration.
Venus Point in Tahiti was named at this time
1) Distance between observers at places A and B
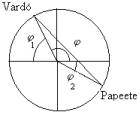
The distance AB can be deduced from the latitudes of the two observing places. In the diagram, φ 1 and φ 2 are the latitudes of A and B, and R is the radius of the Earth.
In the right angled triangle that divides the isosceles triangle RAB
sin ((φ 1 + φ 2 ) / 2) = (AB / 2) / R
Then the distance AB is
AB = 2 R sin ((φ 1 + φ 2 ) / 2)
Be careful! If both cities are in the same hemisphere, the angle is (φ 1 - φ 2 ) / 2 and also the geometrical situation changes if the cities are on different longitudes.
We use observations from 1769, in particular Vardö and Tahiti which were in the visible area. Note that the midnight Sun was visible at Vardö
Vardö (Lapland) and Papeete (Tahiti) are at the same longitude (meridian) and their latitudes are 70° 21' N and 17° 32' S.
Then the geometry of the problem changes and the new angle φ to consider is
φ = (90 - φ 1 ) + 90 + φ 2 = 127° 11'
and using the radius of the Earth R = 6378 km, we calculate
AB = 2 R sin(φ / 2) = 11425 km

Captain James Cook's Expedition to Tahiti (see the InfoSheet for more information)
2) Distance Δβ between two observed paths of Venus
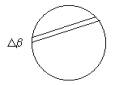
In order to calculate Δβ by direct measurement, we measure the diameter of the Sun D, and the separation of the two paths Δβ, that is to say A'B', on a drawing or a photograph. The angular diameter of the Sun, seen from the Earth is 30' (minutes of arc or 30 / 60°). By means of simple proportion, the separation of the paths is linked to the Sun's diameter by
Δβ / 30' = A'B' / D
therefore
Δβ = (30') (A'B' / D)
but the formula requires the Sun's angular diameter to be expressed in radians. Therefore
Δβ = (30 π / 10800) (A'B' / D)
Δβ = (π /360) (A'B' / D)
Measuring directly the distance between the straight lines 1 and 3, we get Δβ = 1.5 mm and the diameter on the drawing is D = 70 mm, therefore,
Δβ = (π / 360)(1.5 / 70) = 0.00019 radians
If we measure Δβ directly, we introduce an error because it is not easy to measure the separation of the two lines. Students who know Pythagoras' Theorem can use a more accurate method (a more accurate method for measuring Δβ is given in the Appendix 4).
Using the solar parallax we have
β s = 0.38248 Δβ
and using the parallax formula, the distance from the Earth to the Sun r e is
r e = AB / &beta s ;
Using the data from the 1769 expeditions we can calculate the value of r e
r e = 157 10 6 km
It is well know that this value of Earth-Sun distance is currently r e = 149.6 10 6 km. It is possible to get better results using more accurate measurements of Δβ (link 4 a more accurate method for measuring Δβ).
[1] Written by Francis Berthomieu, Frédéric Dahringer, Rainer Gaitzch, Michele Gerbaldi, Alan Pickwick, Rosa M. Ros (EAAE)