The Venus Transit 2004

... Educational Sheet 3

Appendix 4

Calculation of Δβ by measuring chords
(a more accurate method for finding Δβ)

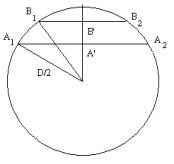
The distance Δβ between the chords A and B is difficult to measure because the two lines are always very close to each other compared to the diameter of the Sun. We can replace the measurement of the separation A'B' by the measurement of the lengths of the chords A 1 A 2 and B 1 B 2 , the transit paths for the observers at A and B.

Using Pythagoras' theorem, we obtain the relation

B'S = 0.5   √(D 2 - B 1 B 2 2 ) A'S = 0.5   √(D 2 - A 1 A 2 2 )

In order to get A'B' we calculate the difference B'S - A'S

A'B' = 0.5   [√(D 2 - B 1 B 2 2 ) - √(D 2 - A 1 A 2 2 )]

Dividing by the diameter D gives

A'B' / D = 0.5   [√(1 - (B 1 B 2 /D) 2 ) - √(1 - (A 1 A 2 /D) 2 )]

Measuring A 1 A 2 , B 1 B 2 and D on the image of the Sun, we obtain A 1 A 2 = 52 mm (line 3), B 1 B 2 = 49 mm (line 1) and D = 70 mm.

Then,

A'B' / D = 0.5   [√(1 - (49 / 70) 2 ) - √(1 - (52 / 70) 2 )] = 0.02235

and Δβ is given by

Δβ = (31 π /360) 0.02235 = 0.00020 radians

Using the parallax formula we have

βs = 0.38248 Δβ

and using the solar parallax formula, the distance from the Earth to the Sun r e is

r e = AB / βs

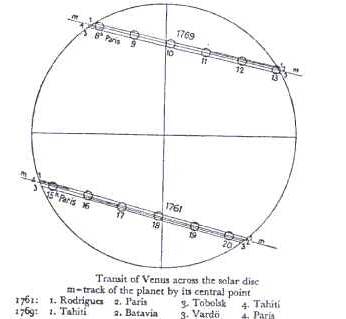
Using the data from the 1769 expeditions and AB = 11425 km we can calculate

r e = 149 10 6 km

As you can see, it is difficult to produce consistent results, although this result is reasonably close to the currently accepted value.

It is very difficult to take accurate measurements of a drawing or a photograph, and this lowers the accuracy of the final result. We suggest a similar method which uses the duration of the transit. This idea is similar to the current observations made by the students (see Appendix 5).

Back to the EduSheet 3