mirror sites:
PL (internal link)
HQ
[?]
mirror sites:
PL (internal link)
HQ
[?]
Quality Control and
Data Processing
|
GIRAFFE: Detector monitoring
Find the description of the current GIRAFFE CCD (named "Carreras", often referred to as "new CCD") here. It replaced in 2008 the "old" detector called "Bruce". Both CCDs are identical in format and size; unless otherwise specified, the content below applies to both CCDs.
2009-01-12: linearity and
gain parameters implemented with detector monitoring data Image flats (also called detector flats) are measured as technical calibrations every 4 weeks or so, as part of the GIRAFFE calibration plan. While the ordinary, daily fibre flats mainly measure fibre characteristics, the image flats are exposures of the CCD by the flat field lamp without the fibre system. Hence, they are used to monitor detector characteristics like
Master image flats are created from a stack of typically 2 input raw frames in order to
Since May 2008, a dedicated template and recipe ("detector monitoring") is in use.  Gain (CONAD)
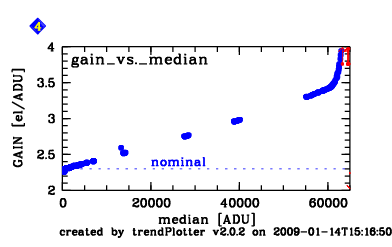
Gain (CONAD)
The conversion factor electrons to ADU (CONAD) is the inverse gain and is also monitored in the linearity trending plot, box 2. It is measured from the difference between two identical raw frames, by comparing the square root of the signal to its measured rms. The mean gain value is given in the plot. Multiple values exist since usually several pairs are available with EXPTIME > 50 sec (e.g. 60 sec, 120 sec, 220 sec).
Correlations. More detailed trending of the gain is available under "correlations" (here, box 4).
The FULL plot shows the gain both for the old and the new CCD. It is observed to be very stable. Scoring&thresholds Gain (CONAD) The gain is very stable in the long-term. It is scored tightly, with fixed values.
- find a pair of image flats having the same exposure level (EXPTIME)  Noise parameters
Noise parameters
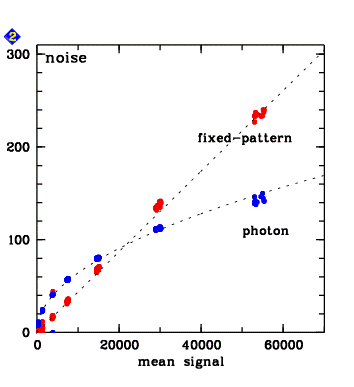
Two kinds of small-scale fluctuations exist in any raw frame: photon noise, and fixed-pattern (gain) noise (the third noise source, read noise, is negligible here). While the photon noise can only be reduced but not removed totally, the gain noise is constant with time and can be entirely removed from science frames using gain maps derived from image flats. Both sources of noise are monitored. They are measured in small subwindows of 100x100 pixels size. They are always checked to be random (Gaussian shape of histogram curve).
The measured fixed-pattern noise of the old CCD is about 0.5% (Fig. 1 of the historical trending plots from 2008 and earlier). It nicely follows a linear slope (Fig. 2 of the trending plot, and also the figure below). The measured photon noise follows a square-root law as expected. The new CCD has a stronger fixed-pattern noise, at the level of about 1.6% (see plots for 2009 and beyond). The noise characteristics are not only relevant for Quality Control, but also interesting for data reduction purpose. Whenever a good S/N is critical, well-exposed gain maps should be used to remove the fixed pattern noise. The penalty to pay is added photon noise, inherent in the image flats. For a single raw flat file obtained with a typical integration time of 220 sec, the turnover from the photon-noise into the gain noise regime is at exposure level 22,000 ADU for the old CCD, see the figure below. For a masterflat stacked from 2 raw frames, photon noise can be reduced by a factor of sqrt(2), and the turnover value is at 11,000 ADU. For a stack made of 3 frames, the critical exposure level is at 7,000 ADU. This means: if high S/N is an issue, one should take care to use gain maps having sufficiently high exposure levels everywhere. In principle it makes sense to attempt a gain noise correction only if the photon noise in the map is lower than the gain noise in the science data. For the new CCD, with its higher fixed-pattern noise, the corresponding values are: 3500 ADU (single frame); 1500 ADU (stack of 2); 1200 ADU (stack of 3). These issues are neglected by the Giraffe pipeline which accepts whatever input master flat is specified. Often this is a reasonable approach since usually master flats are created from 3 input raw frames and well exposed. But some of the GIRAFFE setups have flat fields with rather high dynamics. E.g., a single LR 427.2 flat, being exposed at 110 sec, has parts with just 4,000 ADU and other parts being almost saturated.
Scoring&thresholds Noise parameters The score thresholds are set such as to indicate a sudden change, without any judgement about the average value. Since the gain variations are a CCD property, the observed fluctuations are likely due to slightly instable acquisition conditions. Fixed pattern noise was much stronger in the old CCD than it is in the current one. All input data produced by the template are organized by the detmon recipe in pairs of equal EXPTIME. Then, photon noise and fix-pattern noise is calculated as follows:
photon noise: gain fluctuations:  Linearity
Linearity
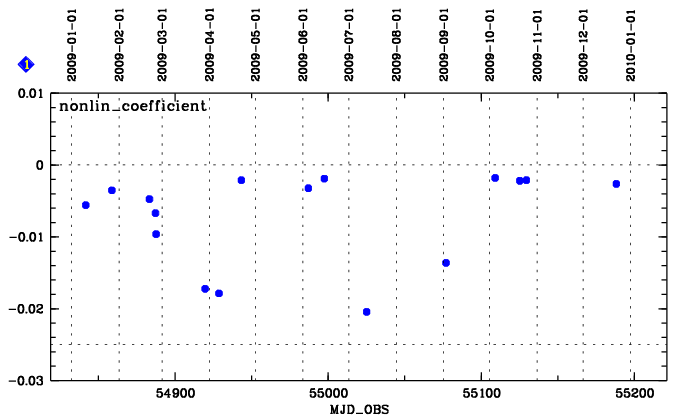
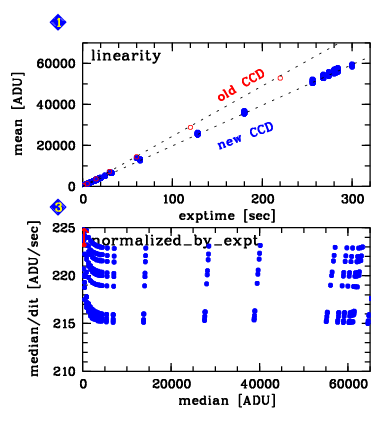
Detector linearity is trended here. A sequence of image flats is exposed between 0.5 and 220 secs. A third-order polynomial is fitted to the mean exposure level as a function of exposure time. An effective non-linearity correction is derived from this and plotted in box 1. This coefficient is derived by the common detector monitoring recipe and is available since 2008-07.
Correlations. More detailed trending of linearity is available under "correlations" (here, boxes 1 and 3). The mean exposure level of all image flats is plotted against the exposure time (box 1). In the example below, data are shown for both the old and the new CCD. A fitted function (broken line) is used to derive residuals which are normalized to the mean and plotted vs. exposure time (box 3). The normalized residuals are below one percent. The shifts of the curves are due to a drifting mean flux level of the calibration lamp.
The linearity coefficient for the new CCD is very stable. Outliers are likely to be due to the complex sequence of image flats to be taken. Whenever after an outlier a new sequence was taken for confirmation, that value was compliant with the long-tem behaviour. The nonlinearity coefficient is scored such as to deliver an alert if it becomes positive or more negative than expected. The thresholds are based on the observed long-term behaviour.
- calculate mean_signal per raw frame  Contamination
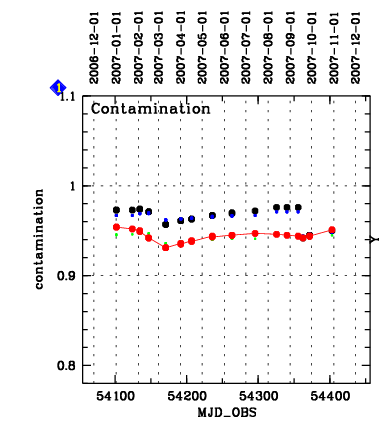
Contamination
The contamination is measured in 5 different windows: 4 in the corners, and one central window. The central window defines the mean signal. The other windows are divided by that number and define the relative signal in that window. The contamination is defined as the relative signal in each of the 4 windows and plotted in report #3.
A potential issue is contamination which is monitored in box 4. A set of four 400x200 pixels subwindows in the corners of the CCD is used to register the intensity there relative to a central reference subwindow. The fraction is trended over time here.
Find a trending plot covering the full history of contamination here. Typically, contamination builds up very slowly and then more strongly. Once the contamination parameter in one of the windows is below 0.9, an intervention is scheduled (heating of the CCD) to bring the CCD efficicency back to its nominal values.
Below find a comparison between the image flats from 2003-04-28 and 2004-06-06 (just before an intervention). A contamination of about 7% has built up in window 4.
Scoring&thresholds Contamination The relative contamination in quadrant #4 is scored. Based on the long-term behaviour, it fires an alert when its value is below 90%. This value is then used to trigger an operational action (decontamination).
- define 4 windows in the corners plus one in the centre |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||