European Southern Observatory (ESO)European Association for Astronomy Education (EAAE) Observatoire de ParisInstitut de Mécanique Céleste et de Calcul des Éphémérides (IMCCE)Astronomical Institute of the Academy of Sciences of the Czech Republic The Venus Transit 2004 European Science & Technology Week 2004Visit the websites of the VT-2004 organisers

The Venus Transit 2004

... Educational Sheet 2


How the Transit of Venus can be used
to determine the Earth-Sun distance [1]


Level: Basic to understanding other concepts; some mathematical ability is required.

Objectives:

  • To understand the concept of parallax, in particular how the parallax angle decreases as the distance increases.
  • To understand the connection between parallax and the transit of Venus

Background:

According to the ability of the students it is possible:

  • to present parallax as a qualitative relationship between parallax angles and distances without introducing numerical relationships. In this case no mathematical background is required.
  • if the teacher wants to achieve numerical results, the students only need to know the definition of the tangent function.

Materials needed:

  • A pole 2 or 2.5 m high (the playground wall or a pole for sporting activities can also be used)
  • Picture (easily visible from several metres)
  • Drinking straws
  • Scotch tape
  • Some thread
  • A fisherman's lead weight
  • Cardboard
  • Split pin
  • Pair of scissors

Resources:

  • A simple quadrant tool
  • A tool to measure horizontal angles

Introduction

About 1690, Edmond Halley observed a transit of Mercury across the Sun. With such a transit, the solar disk forms a bright background for the dark disk of the planet. On account of parallax, the positions on the solar disk must vary for different places on Earth. Since Mercury is very close to the Sun, Halley had the idea that Venus would be more useful for determining the distance. Halley proposed his method in 1691 (Pannekoek, p. 285) with the words: " this will be the only kind of observation that in the next century with the highest precision will disclose the distance from the Sun to the Earth ". He indicated that there would be transits of Venus in 1761 and 1769 (Halley died in 1742).

Parallax is a method for calculating distances. As Venus passes between the Earth and the Sun, the silhouette of its disk can easily be seen through a telescope (with a dark filter).



The transit of Mercury on 7 May 2003. Mercury appears as a small dark circle on the Sun.

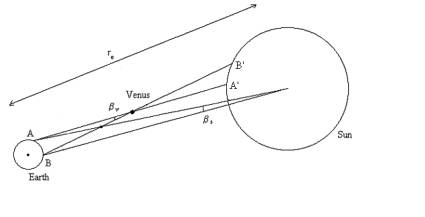
The Sun's circular outline provides a reference against which the parallax of Venus may be measured and the Sun's parallax may be deduced. Astronomers at widespread locations on the Earth observe the transit simultaneously and record the exact time of ingress or egress of Venus across the solar outline. These times differ from observer to observer because of their divergent vantage points. By pooling their timing measurements, astronomers can then calculate the parallax and finally deduce the Earth-Sun distance.

Students can understand this method by measuring the distances to various targets in their environment by parallax. They will first need to build a simple instrument to measure angles. The mathematics needed for this activity is not difficult and trigonometry is not required if they only observe the phenomenon, but can be used if numerical results are desired.


Parallax: a relationship between angles and distances

Students can observe that the parallax angle decreases as the distance to the object increases. If the object is very far away, the parallax angle is very small. We present an experiment to introduce this concept.


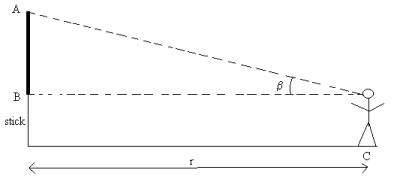
Experiment 1:

By getting relationships between the distance r and the angle β when they observe the object, students find that the angle decreases as the distance to the object increases.

  1. We fix a pole (2 or 2.5 m high) vertically in the school playground.
  2. We mark two points, A and B, on the pole. In order to simplify the mathematics, it is a good idea to mark the point B at 1m or 1.5 m above the ground (roughly the same height as the students that are doing the experiment).
  3. The point A is marked at 1m or 1.5m above B. Then the length AB is known.
  4. The students measure the angle β from the place C using a quadrant (see the Appendix 1) built by themselves.

Depending their age, they can verify:

  • If they make the measurement far away the angle decreases - more distance less parallax.
  • If the students know the definition of the tangent function, they can determine the distance from the point C to the stick by using the length AB and the angle β which it subtends.
    The length AB on the pole is known as is the angle β from the quadrant measurements. By definition,
    tan β = AB / r
    Then they can calculate,
    r = AB / tan β
    Of course the angle gets smaller as the distance r increases. In the case of very small angles it is possible to substitute the angle β for tan β.


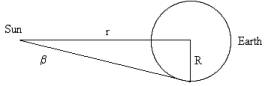
Definition of parallax (the horizontal parallax)

By definition, the parallax of the Sun is the angle β shown below


By trigonometry, tan β = R / r but the angle β is small and tan β can be approximated by β, measured in radians. R is the radius of the Earth and r is the distance from the Earth to the object. We can calculate r using the relationship
r = R / β

The measurement of small angles is a difficult problem when parallax is used to estimate distances. The parallax method can only be used for measuring distances to bodies close to the Earth. For instance, the Sun is too far. Only the Moon, Mars and Venus are accessible.


Scale figure of the Earth, the Moon and their distance apart



Parallax and the Transit of Venus.

Actually, when experiment 1 is carried out, the observer is situated at the vertex of the angle β. We need to compare this situation with the transit of Venus observation.

When the transit is observed from two different places on the Earth, we use the concept of solar parallax βs. This angle cannot be observed, because the observer would have to be situated at the Sun. The value of βs is calculated from the parallax of Venus βv using mathematical relationships. Then the question is, how it is possible to know βv if you cannot observe from Venus. In order to understand how this is possible we must consider a new experiment.


Experiment 2:

When you hold out a finger and view it first with your left eye only and then with your right eye only, your finger seems to shift relative to a distant background. This is the phenomenon of parallax.

Experiment 3:

Raise your finger again to your nose and view a nearby object. Blink your eyes alternately as before and observe the apparent to and fro shift of your finger. Now move your finger a little farther away and blink again. The parallax shift is smaller than it was before. Move your finger even farther and the parallax shift becomes even smaller.
We can deduce the following rule: the farther an object, the smaller is its parallax, and its converse, the smaller the parallax, the farther the object.
Here is the key to measuring the distances of objects around us, from objects a few inches away to stars in outer space.



Measuring distances by parallax with scaled drawings

Experiment 4:

To get a practical approach to the transit situation we try to study the previous experiments from a geometrical point of view.

We have to focus on remote markers behind the object of which we want to estimate the distance.
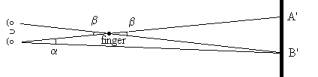
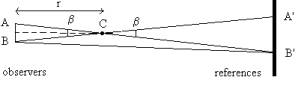
We have to construct a triangle, but in a way differing slightly from the triangulation example (see the Appendix 3). To keep it simple, we try to measure the distance from our eyes to a finger of our outstretched arm. Look with your right eye at the finger, and focus on a marker on the wall or beyond, that is just behind the finger and remember that marker (A_). Now look at your finger with your left eye: another marker (B') will now be behind your finger. If you open and close each of your eyes alternately, your finger will seem to shift from the marker A' to B' and back again.
This is the phenomenon of parallax, and β is the parallax angle of your finger.

When you focus directly on the markers A' and B' (not on the finger), you can easily measure the angle α with your angle-measuring tool (see the Appendix 2). The situation is as shown in the drawing below.


In the drawing, the angle α is somewhat smaller than β, but the farther away are the markers, the more and more similar are the angles α and _. So when you measure _, you know the parallax angle of your finger. When you take the separation of your eyes as the baseline, you can draw to scale the whole triangle and you can measure directly with a ruler the distance from you eyes to your finger.

You can do this experiment in reality. Measure the distance between your eyes with a ruler. Measure α with your angle-measuring tool (see the Appendix 2). You can take markers on the wall of your classroom, but also markers you see outside through the window. Make a scale drawing and use it to find the distance between your eyes and your finger. Check your answer by measuring this distance directly with a ruler or a tape measure.



Experiment 5:

Now you can use the same method outdoors, for instance to measure the distance of a tree. This time you don't use the distance between your eyes as the baseline, but a larger one, like the distance between two vantage points, eventually not visible from each other. From those points two observers at the same time (or the same observer at two different times) have to look at a remote object (a marker) on the horizon that is in line with their position and the tree. Each of them focuses on a specific marker in line with the tree: for one observer the marker will be A', for the other B'. Then they exchange the information about the markers and they can both measure directly the angle (see the Appendix 2) between those two markers, the parallax of the tree. The length of the baseline and the parallax angle give again a triangle that can be drawn to scale in order to derive the distance of the tree.

Notice that this method works also when the observers can't see each other! They both need to be able to see the tree and the markers A' and B' on the horizon.

This method was first used to determine the distance to the Moon. Between 1671 and 1673, Richer, Picard and Cassini used this method to determine the distance to Mars. They chose a time when Mars was as near as possible to the Earth. It is important that:

  • the two observers are as far as possible from each other
  • to use stars as markers
  • to notice at exactly the same time which star, from each position, is covered by Mars
  • to make the observations when Mars is closest to the Earth

When students understand trigonometry, they can use the same measurements to make calculations.


Calculating distances by parallax trigonometrically


Using trigonometry, in particular the definition of tangent, in one of the right angle triangles on the left,
r = (AB/2)/ (tan β/2)
since the angle β is small, tan β can be approximated by β measured in radians and the formula can be simplified,
r = AB/ β
Notice that you can't measure β directly but by using several mathematical relationships during the transit of Venus, the parallax can be calculated (see EduSheet 3).


[1] Written by Leonarda Fucili, Rupert Genseberger, Rosa M. Ros (EAAE)