DATABASE OF TECHNICAL DATA
BACKGROUND MODEL
The background brightness and its dependence on wavelength are modeled in the following way:
i.e. as the sum of a (pseudo-)continuum, emission lines, thermal atmospheric emission and thermal emission from the telescope (and instrument). Below each of these components is discussed in turn. Atmospheric extinction is also discussed here.
Continuum
In the blue-optical the background brightness is dominated by the continuum which has contributions from a number of sources, chiefly: diffuse galactic emission, zodiacal light and moonlight scattered by the atmosphere. Hence, in practice the background brightness at a given wavelength and at a given position in the sky depends on a number of parameters, including the position's location with respect to the galaxy, ecliptic and moon, the moon phase, the phase of the solar cycle, the season, the observatory's geomagnetic latitude and airmass. Compared to the darkest possible background most of these systematic effects increase the background by up to several tenths of a magnitude. The moon has the largest effect – up to several magnitudes in the blue. In addition, even when all known systematic effects are accounted for, the background brightness still fluctuates by ~0.2 mag on timescales of minutes, hours and nights. Unfortunately, even if we concentrate only on the most prominent effect (the moon) and ignore all others, an accurate model of the background brightness still requires a fair amount of complexity. This is being investigated.
For now our background model simply adopts an empirical value for the continuum that remains constant in each band. For the UBVRI bands these continuum values correspond to the broadband brightnesses as given by the standard ESO ETC sky brightness table for a moon phase of 3 days from new moon. Any dependencies on the site and airmass are ignored.
In the near-IR the background brightness is dominated by the emission line component (mostly OH airglow) and hence the standard broadband sky brightnesses are inappropriate for the inter-line (pseudo-)continuum. Instead the model uses the continuum values measured with ISAAC by Cuby et al. (2000) in the J and H bands. The H-band value is also used in the K-band, beyond which the continuum is irrelevant. However, note that these values are highly uncertain and may depend on the details of the spectrograph. The true continuum may be significantly lower (e.g. Ellis & Bland-Hawthorn 2008). All continuum values are summarised in the following table:
| Filter | Continuum brightness | Comment | |
|---|---|---|---|
| [γ/s/μm/m2/arcsec2] | [mag/arcsec2] | ||
| U | 190 | 21.5 | Standard ESO ETC sky brightness table for 3 days from new moon |
| B | 150 | 22.4 | |
| V | 210 | 21.7 | |
| Rc | 340 | 20.8 | |
| Ic | 500 | 19.9 | |
| J | 1200 | 18.0 | Cuby et al. |
| H | 2300 | 16.5 | |
| K | 2300 | 15.7 | |
Emission lines
The emission lines (OH airglow) dominate the background in the near-IR, i.e. in the JHK bands. Although the airglow does not depend on moon phase it is known to vary systematically as a function of season and time of night, as well as randomly on shorter timescales and as a function of position on the sky. We have not attempted to model this and so the OH lines are always assumed to have the same strength. In particular, we have not (yet) included in the model any dependence of the OH airglow on the site or airmass.
This data file contains a compilation of optical and near-IR emission lines. The optical lines (λ < 0.92 μm) are from the UVES sky emission atlas (Hanuschik 2000; online data) while the near-IR lines are from the atlas of OH lines (Rousselot et al. 2000). The first column contains the line wavelength in μm and the second column contains the line flux (integrated over wavelength) in photons/s/m2/arcsec2.
Atmospheric emission
From the second half of the K-band onwards the background is dominated by the thermal emission from the atmosphere and the telescope. The atmospheric emission was calculated by A. Smette using the HITRAN molecular database and assuming a tropical atmospheric profile. Molecules included are: H2O, CO, CO2, CH4, O2, O3 and N2O. The calculations were performed for four different values of airmass and for each of these sites.
These data files contain the atmospheric emission spectra for the various combinations of site, airmass and wavelength region (0.4 – 30 μm). The resolution of these spectra is 100,000.
Telescope emission
The emission from the telescope is modeled as a grey body (i.e. a black body multiplied by a constant emissivity ε). The telescope's emissivity is given here and its temperature is that of the site's ambient temperature.
Discussion
The background model is shown in Figs. 1-3 below at a resolution of R = 1000. The faint grey line in each of the figures shows a similar model from the Gemini Exposure Time Calculator for Mauna Kea. The comparison highlights some of the uncertainties. The differences in the blue-optical are mainly due to different assumptions regarding the amount of the moonlight, although the Gemini model also rises quite steeply towards the red which is difficult to explain with just the moon. In the near-IR the model (pseudo-)continua are also different in shape (Fig. 2). The Gemini model assumes that the continuum is due to zodiacal light which is modeled by a grey body with a temperature of 5800 K and which is subject to atmospheric extinction. However, the normalisation is far too high for zodiacal light (by a factor of ~70) and must be arbitrarily cut off near 0.9 μm in order to avoid producing far too much background light in the optical. The agreement in the OH lines, on the the other hand, is reasonable, and the apparent differences are mainly due to resolution. Note that the Gemini model does not include a telescope component. Hence the rise in the the second half of the K-band is solely due to the atmosphere.
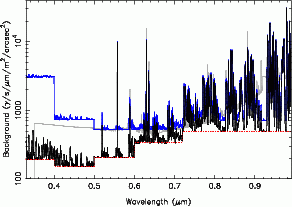 |
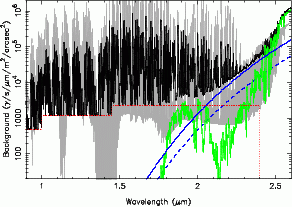 |
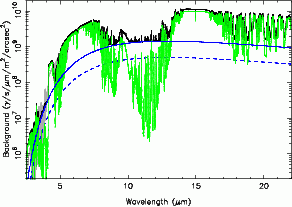 |
| Fig. 1 | Fig. 2 | Fig. 3 |
Atmospheric extinction
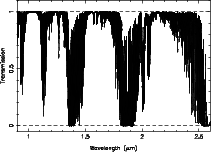
Atmospheric extinction is due to (at least) two different processes: molecular absorption and scattering by molecules and aerosols. The absorption is calculated by the same atmospheric model already described above, again for all combinations of airmass and site. Since scattering is only effective in the blue-optical, where molecular absorption is almost absent, we use a standard Paranal blue-optical extinction curve to represent the effect of scattering. The combined, total atmospheric transmission is hence given by
where ξabs(λ) is given by the atmospheric model, χ is the airmass and k(λ) is the extinction coefficient (= 0 for λ > 0.7 μm). For the High and Dry site the Paranal extinction curve is multiplied by 0.6 (Giraud et al. 2006). The combined, total atmospheric transmission is shown in Figs. 4–6.
Data files
containing ξabs(λ).
Data files
containing k(λ).
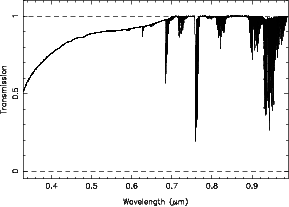 |
 |
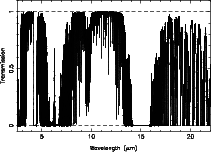 |
| Fig. 4 | Fig. 5 | Fig. 6 |
E-ELT Science
What's New?
- 05 Dec 2014
Spending on first construction phase approved
Science Case
Project Science Team
Phase B (2006 – 2011)
- Science Working Group
- Design Reference Mission
- Design Reference Science Plan
- Tools: Imaging ETC / Spectroscopic ETC / Other software
